Etape 1 : Examiner les valeurs calculées
En utilisant les valeurs des deux variables de fonction de puissance que vous avez entrées, Minitab calcule le nombre de répétitions, la valeur de la différence maximale entre les moyennes des effets principaux ou la puissance du plan.
- Valeurs de la différence maximale entre les moyennes des effets principaux
- La différence maximale est la différence à détecter entre les niveaux de facteurs ayant les plus petites et les plus grandes moyennes. Les calculs utilisent le facteur comportant le plus grand nombre de niveaux pour produire des calculs prudents pour les autres facteurs. Minitab calcule la plus petite différence que le plan détecte. Un plus grand nombre de répétitions permet au plan de détecter de plus petites différences. En général, vous voulez pouvoir détecter la plus petite différence ayant des conséquences pratiques pour votre application.
- Répliques
- Si vous entrez la valeur de la différence maximale entre les moyennes des effets principaux et la valeur de puissance, Minitab calcule le nombre de répétitions. On parle de répétitions lorsque plusieurs essais expérimentaux sont effectués avec les mêmes paramètres de facteurs. Etant donné que le nombre de répétitions est une valeur entière, la puissance réelle peut être légèrement supérieure à votre valeur cible.
- Nombre total d'essais
- Pour tous les cas, Minitab calcule le nombre total d'essais à partir du nombre de répétitions. Le nombre d'essais dans une seule répétition est le produit des nombres de niveaux. Le nombre total d'essais est le produit de la taille de ce plan de base et du nombre de répétitions.
- Valeurs de puissance
- Si vous entrez le nombre de répétitions et la différence maximale entre les moyennes des effets principaux, Minitab calcule la valeur de puissance. La puissance est la probabilité selon laquelle vous détecterez correctement une différence significative. Une valeur de puissance 0,9 est généralement suffisante. Une valeur de 0,9 indique qu'il existe une probabilité de 90 % qu'une différence soit détectée entre les paramètres de facteurs. Avec d'autres propriétés de plan demeurant constantes, lorsque le nombre total d'essais est moins élevé ou que la valeur maximale est plus petite, le plan offre moins de puissance.
Résultats
| Différence maximale | Répliques | Nombre total d'essais | Puissance cible | Puissance réelle |
|---|---|---|---|---|
| 2,0 | 3 | 108 | 0,8 | 0,932615 |
| 2,0 | 3 | 108 | 0,9 | 0,932615 |
| 1,8 | 3 | 108 | 0,8 | 0,867493 |
| 1,8 | 4 | 144 | 0,9 | 0,952918 |
Résultats principaux : différence maximale, répétitions, nombre total d'essais, puissance cible et puissance réelle
Dans ces résultats, Minitab calcule le nombre de répétitions nécessaires pour atteindre une puissance cible de 80 % et une puissance cible de 90 %. Pour détecter une différence de 2,0, le plan nécessite 3 répétitions pour atteindre la cible de 80 % ou de 90 %. La puissance pour le plan avec 2 répétitions est inférieure à la puissance cible de 80 %. Pour détecter la plus petite différence de 1,8, 3 répétitions donnent une puissance de plus de 80 %, mais pas de plus de 90 %. Pour détecter la plus petite différence avec une puissance de 90 %, l'expérience conçue nécessite 4 répétitions. Etant donné que les nombres de répétitions sont des entiers, les puissances réelles sont supérieures aux puissances cible.
Ces résultats indiquent également que le facteur avec le plus de niveaux en comporte 4. Ces résultats sont exacts pour le facteur à 4 niveaux. Le nombre de répétitions peut être différent pour les deux facteurs à 3 niveaux, particulièrement si la puissance réelle excède de beaucoup la puissance cible.
Etape 2 : Examiner la courbe de puissance
La courbe de puissance vous permet d'évaluer les propriétés adaptées pour le plan.
La courbe de puissance représente la relation entre la puissance et la différence maximale pour chaque nombre de répétitions. Chaque symbole sur la courbe de puissance représente une valeur calculée en fonction des propriétés saisies. Par exemple, si vous entrez un nombre de répétitions et une valeur de puissance, Minitab calcule la différence maximale correspondante et affiche la valeur calculée sur le graphique.
Examinez les valeurs sur la courbe pour déterminer la différence entre la plus grande et la plus petite moyenne pour le facteur ayant le plus de niveaux détectés par l'expérience à une valeur de puissance et un nombre de répétitions spécifiques. La valeur de puissance 0,9 est généralement appropriée. Toutefois, certains spécialistes considèrent que la valeur 0,8 est adéquate. Si un plan offre une puissance inférieure, il se peut que vous ne puissiez pas détecter une différence significative sur le plan pratique. L'augmentation du nombre total d'essais expérimentaux augmente la puissance du plan. Le plan doit contenir suffisamment d'essais expérimentaux pour atteindre une puissance adéquate. Un plan offre une plus grande puissance de détection d'une différence supérieure que d'une différence inférieure.
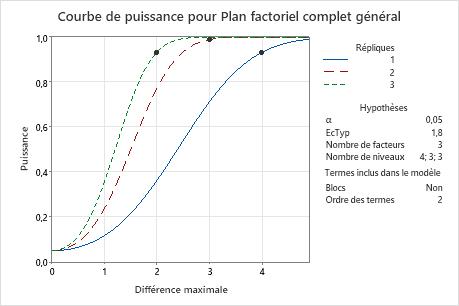
Dans ces résultats, Minitab calcule le nombre de répétitions pour atteindre une puissance d'au moins 0,9 pour les différences maximales de 2, 3 ou 4. Le diagramme présente une courbe pour chaque nombre de répétitions. Pour détecter une différence maximale de 2 avec une puissance d'au moins 0,9, le plan nécessite 3 répétitions. Le diagramme contient une courbe pour 3 répétitions et inclut un symbole à une différence maximale de 2, où la puissance excède 0,9. Pour détecter une différence maximale de 3 avec une puissance d'au moins 0,9, le plan nécessite 2 répétitions. Pour une différence maximale de 4 avec une puissance d'au moins 0,9, le plan nécessite 1 répétition.
