Méthodes et formules pour Puissance et effectif de l'échantillon pour le plan factoriel à 2 niveaux

Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Calcul de la puissance
Calcul des répétitions, des effets et des points centraux
Paramètre de non-centralité

Calcul de la puissance

Minitab suppose qu'il n'existe aucun facteur de texte et donc aucun pseudo-point central.

Minitab calcule d'abord les degrés de liberté pour l'erreur (v).

Degrés de liberté pour l'erreur: ν = (nombre total d'observations – nombre de paramètres estimés); nombre total d'observations = n * r + cptotal; nombre de paramètres estimés = nombre de sommets uniques par répétition + 1 (si le terme pour les points centraux est inclus) + nombre des paramètres pour les blocs (si les blocs sont dans le modèle) – nombre de termes omis du modèle – nombre de termes factoriels confondus avec des blocs; Le nombre de paramètres pour les blocs est b-1. Si n = b ou si n/b est un entier, aucun terme factoriel n'est confondu avec des blocs.; Si n/b n'est pas un entier, chaque bloc ne comporte qu'une fraction 1/2^q du plan de base. Soit q le plus petit entier pour lequel n est un multiple de b/2^q, alors les termes factoriels 2^q – 1 sont confondus avec des blocs.
Puissance

Notation

Terme	Description
k	nombre de facteurs
r	nombre d'essais aux sommets par répétition
n	nombre de répétitions
b	nombre de blocs (si aucun bloc n'existe, b = 1))
σ	écart type estimé
δ	effet
α	seuil de signification
v	degrés de liberté pour l'erreur
λ	paramètre de non-centralité
f_α	valeur critique (α supérieure pour une loi F avec 1 et ν degrés de liberté)
F(f_α ; 1, v, λ)	CDF de la loi F avec 1 degré de liberté du numérateur, v degrés de liberté du dénominateur et le paramètre de non-centralité λ, évaluée à f_α
cpblock	nombre de points centraux par bloc
cptotal	nombre total de points centraux = b * cpblock

Calcul des répétitions, des effets et des points centraux

Si vous fournissez les valeurs pour la puissance et deux autres propriétés, Minitab calcule la quatrième propriété inconnue en appliquant l'équation de puissance de façon itérative. A chaque itération, Minitab détermine la puissance pour les valeurs des propriétés fournies et une valeur d'essai de la statistique que vous n'avez pas indiquée. Minitab s'arrête lorsque l'algorithme atteint la valeur de puissance indiquée.

Lorsque vous indiquez une valeur de puissance, Minitab peut déterminer qu'aucun nombre entier de répétitions ne génère la puissance cible. Dans de tels cas, Minitab affiche la valeur cible de la puissance à côté de la puissance réelle pouvant être atteinte en fonction de vos spécifications. La puissance réelle est la valeur la plus proche de la puissance cible, tout en lui étant supérieure.

Paramètre de non-centralité

Formule

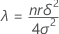
Notation

Terme	Description
r	nombre d'essais aux sommets par répétition
n	nombre de répétitions
σ	écart type estimé
δ	effet
λ	paramètre de non-centralité