Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
Calcul de la puissance avec la méthode de Levene
La fonction de puissance pour un test de variance est Q(ρ) = P (Reject H0 | ρ).
Puissance unilatérale (H1 : σ1 / σ2 < 1
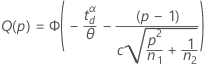
Puissance unilatérale (H1 : σ1 / σ2 > 1)
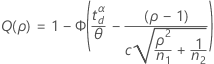
Bilatérale (H1 : σ1 / σ2 ≠ 1
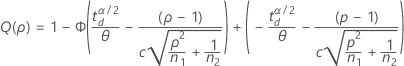
Notation
| Terme | Description |
|---|---|
| Φ | CDF de la loi normale standard |
| tα d | percentile supérieur de la loi T avec d = n1 + n2 – 2 degrés de liberté |
| θ | 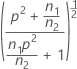 |
| c |  |
| ρ | σ 1 / σ 2 |
| n 1 | effectif du premier échantillon |
| n 2 | effectif du second échantillon |
Calcul de la puissance avec la méthode du test F
Formule
La fonction de puissance pour un test de variance est Q(ρ) = P(Reject H0 | ρ).
Puissance unilatérale (H1 : σ1 / σ2 < 1)
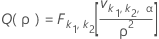
Puissance unilatérale (H1 : σ1 / σ2 > 1)
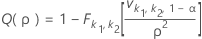
Puissance bilatérale (H1 : σ1 / σ2 ≠ 1)
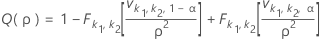
Notation
| Terme | Description |
|---|---|
| F k 1, k 2 | fonction de répartition de la loi F avec k1 et k2 degrés de liberté |
| v k 1, k 2, A | CDF inverse évaluée à A pour une loi F avec k 1 et k 2 degrés de liberté |
| k 1 | n – 1 |
| k2 | n – 1 |
| α | seuil de signification |
| ρ | σ 1 / σ 2 |
Calcul de la puissance à l'aide de la méthode de Bonett
Remarque
Pour calculer la puissance pour la méthode de Bonett, utilisez la commande de session POWER avec les sous-commandes TWOVARIANCE et BONETT.
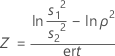

Puissance unilatérale (H1 : σ1 / σ2 < 1)
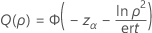
Puissance unilatérale (H1 : σ1 / σ2 > 1)
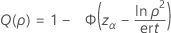
Puissance unilatérale (H1 : σ1 / σ2 ≠ 1)

Notation
| Terme | Description |
|---|---|
| Si | écart type de l'échantillon i |
| ρ | rapport des écarts type de population (s1 / s2) |
| ert | erreur type |
| γ | aplatissement commun réel des populations parent (γ n'est pas l'excès de l'aplatissement) |
| n | effectif de l'échantillon (pour les calculs de puissance, n est supposé être le même pour les deux échantillons) |
| Φ | fonction de répartition pour la loi normale standard |
| α | seuil de signification pour le test |
| zi | point de percentile supérieur i pour la loi normale standard |
Calcul de l'effectif de l'échantillon et du rapport
Si vous indiquez les valeurs de la puissance et l'effectif de l'échantillon, Minitab calcule la valeur du rapport. Si vous indiquez les valeurs de la puissance et du rapport, Minitab calcule la valeur de l'effectif de l'échantillon.
Pour ces deux cas, Minitab utilise un algorithme itératif avec l'équation de puissance. A chaque itération, Minitab détermine la puissance pour l'effectif d'échantillon ou le rapport d'un essai, et il s'arrête lorsqu'il atteint les valeurs que vous avez demandées.
Puissance cible et puissance réelle
Lorsque Minitab calcule l'effectif de l'échantillon, il peut déterminer qu'aucune valeur d'entier de l'effectif de l'échantillon ne génère la puissance cible. Dans ces cas, Minitab affiche la valeur cible de la puissance à côté de la puissance réelle, qui correspond à une valeur d'entier de l'effectif de l'échantillon, la plus proche de la valeur cible, tout en lui étant supérieure.
