Un ingénieur travaillant pour une société de soins optiques teste une nouvelle solution nettoyante pour lentilles de contact. Elle souhaite vérifier que cette nouvelle solution nettoie les lentilles de contact aussi bien que celle de leur marque phare. L'ingénieur fait porter des lentilles de contact à 14 participants pendant une journée, puis leur demande de les nettoyer. Chaque participant nettoie une lentille avec la nouvelle solution et l'autre lentille avec la solution de marque phare. L'ingénieur évalue la propreté de chaque lentille en mesurant l'angle de contact d'une goutte de solution sur les lentilles. L'angle de contact est influencé par le film ou les dépôts sur la lentille. Pour qu'il y ait équivalence, l'angle moyen obtenu avec la nouvelle solution ne doit pas s'écarter de plus de 0,5 degrés de celui obtenu avec la solution de marque phare.
Avant de collecter les données pour le test d'équivalence avec données appariées, l'ingénieur effectue un calcul de puissance et d'effectif d'échantillon afin de déterminer si un effectif d'échantillon de 14 offre une puissance adaptée pour le test. En se fondant sur de précédents échantillons, l'ingénieur estime l'écart type de la population à 0,42.
- Sélectionnez .
- Dans la fonction Hypothèse sur, sélectionnez Moyenne du test - moyenne de référence (différence).
- Dans la fonction Que souhaitez-vous déterminer ? (Hypothèse alternative), sélectionnez Limite inférieure < moyenne du test - moyenne de référence < limite supérieure.
- Dans la zone Limite inférieure, saisissez -0,5. Dans la zone Limite supérieure, saisissez 0,5.
- Dans la zone Effectifs des échantillons, saisissez 14.
- Dans la zone Différences (dans les limites), saisissez 0,1 0,2 0,3 0,4.
- Dans la zone Ecart type des différences pour données appariées, saisissez 0,42.
- Cliquez sur OK.
Interprétation des résultats
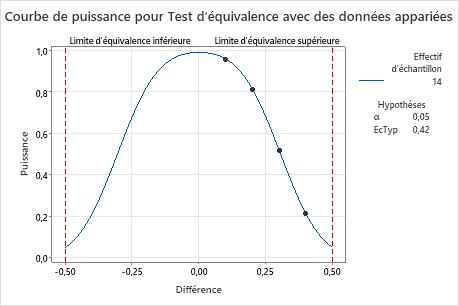
Si la différence est de 0,1 et que l'ingénieur utilise un effectif d'échantillon de 14 paires d'observations, la puissance du test est supérieure à 0,9. Si la différence est de 0,2 et que l'ingénieur utilise un effectif d'échantillon de 14 paires d'observations, la puissance du test dépasse 0,8. Toutefois, si la différence est de 0,3 et que l'ingénieur utilise un effectif d'échantillon de 14 paires d'observations, la puissance du test est d'approximativement 0,52, ce qui n'est pas une valeur adéquate.
Plus la différence est proche de la limite d'équivalence supérieure (0,5), plus la puissance du test diminue. Par exemple, pour une différence de 0,4, si l'ingénieur utilise un effectif d'échantillon de 14 paires d'observations, la puissance du test est d'approximativement 0,22.
Pour tout effectif d'échantillon, lorsque la différence se rapproche de la limite d'équivalence inférieure ou supérieure, la puissance du test diminue et se rapproche de α (alpha, qui représente le risque de déclarer l'équivalence alors qu'elle n'existe pas).
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -0,5 ou différence ≥ 0,5 |
| Hypothèse alternative : | -0,5 < différence < 0,5 |
| Niveau α : | 0,05 |
Résultats
| Différence | Effectif d'échantillon | Puissance |
|---|---|---|
| 0,1 | 14 | 0,957371 |
| 0,2 | 14 | 0,811858 |
| 0,3 | 14 | 0,517255 |
| 0,4 | 14 | 0,211869 |