Sur ce thème
Puissance pour la différence
La première ligne du résultat indique comment les hypothèses sont indiquées pour le test d'équivalence.
"Puissance pour la différence" indique que les hypothèses sont indiquées en matière de différence entre la moyenne de la population du test et la moyenne de la population de référence par transformation logarithmique (moyenne du test – moyenne de référence).
Puissance pour le rapport
La première ligne du résultat indique comment les hypothèses sont indiquées pour le test d'équivalence.
"Puissance pour le rapport" indique que les hypothèses sont indiquées en matière de rapport entre la moyenne de la population du test et la moyenne de la population de référence par transformation logarithmique (moyenne du test/moyenne de référence).
Hypothèse nulle et hypothèse alternative
- Hypothèse nulle
- Minitab teste une ou les deux hypothèses nulles suivantes, en fonction de l'hypothèse alternative que vous avez sélectionnée :
- La différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est supérieure ou égale à la limite d'équivalence supérieure.
- La différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est inférieure ou égale à la limite d'équivalence inférieure.
- Hypothèse alternative
- L'hypothèse alternative stipule une ou les deux affirmations suivantes :
- La différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est inférieure à la limite d'équivalence supérieure.
- La différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est supérieure à la limite d'équivalence inférieure.
Interprétation
Utilisez les hypothèses nulle et alternative pour vous assurer que les critères d'équivalence sont corrects et que vous avez sélectionné l'hypothèse alternative appropriée à tester.
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -0,425 ou différence ≥ 0,425 |
| Hypothèse alternative : | -0,425 < différence < 0,425 |
| Niveau α : | 0,05 |
Dans ces résultats, Minitab teste deux hypothèses nulles :
- La différence entre la moyenne de la population du test et la moyenne de la population de référence est inférieure ou égale à la limite d'équivalence inférieure de −0,425.
- La différence entre la moyenne de la population du test et la moyenne de la population de référence est supérieure ou égale à la limite d'équivalence supérieure de 0,425.
α (alpha)
Le niveau de signification (dénoté par alpha ou α) est le niveau maximal acceptable du risque de rejet de l'hypothèse nulle lorsqu'elle est vraie (erreur de type I). Par exemple, si vous effectuez un test d'équivalence en utilisant les hypothèses par défaut, un α de 0,05 indique un risque de 5 % de déclarer l'équivalence alors que la différence entre la moyenne du test et la moyenne de référence n'est pas réellement comprise dans les limites d'équivalence.
Le niveau α pour un test d'équivalence détermine également le niveau de confiance pour l'intervalle de confiance. Le niveau de confiance par défaut est (1 – α) x 100 %. Si vous utilisez la méthode alternative du calcul de l'intervalle de confiance, le niveau de confiance est (1 – 2α) x 100 %.
Interprétation
Le seuil de signification permet de minimiser la valeur de puissance du test lorsque l'hypothèse nulle (H0) est vraie. Des valeurs plus élevées du seuil de signification donnent au test davantage de puissance, mais augmentent également les chances de faire une erreur de type I, c'est-à-dire de rejeter à tort l'hypothèse nulle alors qu'elle est vraie.
Ecart type supposé pour chaque sujet
L'écart type supposé pour chaque sujet est l'écart type des valeurs de réponse du même participant. Cette mesure de l'écart type détermine l'ampleur de l'erreur aléatoire dans les mesures de réponse du même participant après avoir éliminé les effets de traitement, les effets de période et les effets systématiques. Des valeurs supérieures indiquent une variabilité plus importante dans les valeurs de réponse de chaque participant.
Interprétation
Si vous effectuez une analyse de puissance pour un test d'équivalence sur la différence, vous devez entrer l'écart type pour chaque sujet. L'écart type supposé pour chaque sujet est une estimation de l'écart type de la population.
Minitab utilise l'écart type supposé pour chaque sujet afin de calculer la puissance du test. Des valeurs plus élevées de l'écart type pour chaque sujet indiquent une plus grande variation, ou "bruit", dans les données, ce qui diminue la puissance statistique d'un test.
Coefficient de variation supposé pour chaque sujet
Le coefficient de variation supposé pour chaque sujet est le coefficient de variation de plusieurs valeurs de réponse du même participant. Le coefficient de variation est égal à l'écart type divisé par la moyenne.
Cette mesure de la variation détermine l'ampleur de l'erreur aléatoire dans les mesures de réponse du même participant après avoir éliminé les effets de traitement, les effets de période et les effets systématiques. Des valeurs supérieures indiquent une variabilité plus importante dans les valeurs de réponse de chaque participant.
Interprétation
Si vous effectuez une analyse de puissance pour un test d'équivalence sur le rapport, vous devez entrer le coefficient de variation pour chaque sujet. Ce coefficient de variation supposé pour chaque sujet est une estimation du coefficient de variation de la population.
Minitab utilise le coefficient de variation supposé pour chaque sujet pour calculer la puissance du test. Des valeurs plus élevées du coefficient de variation supposé pour chaque sujet indiquent une plus grande variation, ou "bruit", dans les données, ce qui diminue la puissance statistique d'un test.
Différence
Cette valeur représente la différence entre la moyenne de la population de test et la moyenne de la population de référence.
Remarque
Les définitions et l'interprétation dans cette rubrique sont applicables à un test d'équivalence type utilisant l'hypothèse alternative par défaut (Limite inférieure < moyenne du test - moyenne de référence < limite supérieure).
Interprétation
Si vous entrez l'effectif de l'échantillon et la puissance du test, Minitab calcule la différence pouvant être adaptée par le test à la puissance et à l'effectif d'échantillon indiqués. Pour des effectifs d'échantillons plus grands, la différence peut être plus proche des limites d'équivalence.
Pour examiner plus en détail la relation entre l'effectif de l'échantillon et la différence, pouvant être adaptée par le test à une puissance donnée, utilisez la courbe de puissance.
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -0,425 ou différence ≥ 0,425 |
| Hypothèse alternative : | -0,425 < différence < 0,425 |
| Niveau α : | 0,05 |
Résultats
| Effectif d'échantillon | Puissance | Différence |
|---|---|---|
| 4 | 0,9 | -0,278474 |
| 4 | 0,9 | 0,278474 |
| 8 | 0,9 | -0,329164 |
| 8 | 0,9 | 0,329164 |
| 12 | 0,9 | -0,348248 |
| 12 | 0,9 | 0,348248 |
Ces résultats montrent comment l'augmentation de l'effectif de l'échantillon augmente l'importance de la différence pouvant être adaptée à un niveau de puissance donné :
- Avec 4 participants dans chaque séquence, la puissance du test est d'au moins 0,9 lorsque la différence est comprise entre environ −0,278 et 0,278.
- Avec 8 participants dans chaque séquence, la puissance du test est d'au moins 0,9 lorsque la différence est comprise entre environ −0,329 et 0,329.
- Avec 12 participants dans chaque séquence, la puissance du test est d'au moins 0,9 lorsque la différence est comprise entre environ −0,348 et 0,348.
Rapport
Cette valeur représente le rapport entre la moyenne de la population de test et la moyenne de la population de référence. Pour effectuer des calculs de puissance pour un rapport, vous devez sélectionner une hypothèse sur Moyenne du test / moyenne de référence (rapport, par transformation log).
Remarque
Les définitions et l'interprétation dans cette rubrique sont applicables à un test d'équivalence utilisant l'hypothèse alternative par défaut pour le rapport (Limite inférieure < moyenne du test / moyenne de référence < limite supérieure).
Interprétation
Si vous entrez l'effectif de l'échantillon et la puissance du test, Minitab calcule les rapports minimal et maximal pouvant être adaptés par le test à la puissance et à l'effectif d'échantillon indiqués. Pour des effectifs d'échantillons plus grands, le rapport peut être plus proche des limites d'équivalence.
Pour examiner plus en détail la relation entre l'effectif de l'échantillon et les rapports, pouvant être adaptée par le test à une puissance donnée, utilisez la courbe de puissance.
Méthode
| Puissance pour le rapport : | Moyenne du test / moyenne de référence |
|---|---|
| Hypothèse nulle : | Rapport ≤ 0,9 ou rapport ≥ 1,1 |
| Hypothèse alternative : | 0,9 < rapport < 1,1 |
| Niveau α : | 0,05 |
Résultats
| Effectif d'échantillon | Puissance | Rapport |
|---|---|---|
| 10 | 0,9 | 0,91749 |
| 10 | 0,9 | 1,07903 |
| 20 | 0,9 | 0,91207 |
| 20 | 0,9 | 1,08544 |
Ces résultats montrent comment l'augmentation de l'effectif de l'échantillon augmente la plage des rapports pouvant être adaptée à un niveau de puissance donné :
- Avec 10 observations dans chaque séquence, la puissance du test est d'au moins 0,9 lorsque le rapport est compris entre environ 0,92 et 1,08.
- Avec 20 observations dans chaque séquence, la puissance du test est d'au moins 0,9 lorsque le rapport est compris entre environ 0,91 et 1,09.
Effectif échantillon
L'effectif de l'échantillon correspond au nombre total d'observations dans l'échantillon. Pour une étude croisée 2x2, l'effectif de l'échantillon représente le nombre de participants dans chaque séquence de l'étude.
Interprétation
Utilisez l'effectif de l'échantillon pour déterminer le nombre d'observations nécessaires pour obtenir une certaine valeur de puissance pour le test d'équivalence à une différence spécifique.
Si vous indiquez une différence (ou un rapport) et une valeur de puissance pour le test, Minitab calcule l'effectif d'échantillon nécessaire. Etant donné que les effectifs d'échantillons sont des nombres entiers, la puissance réelle du test peut être légèrement supérieure à la valeur de puissance que vous avez indiquée.
Si vous augmentez l'effectif de l'échantillon, la puissance du test augmente également. L'échantillon doit contenir suffisamment d'observations pour atteindre une puissance adéquate. Toutefois, si l'effectif de l'échantillon est trop grand, vous risquez de gaspiller du temps et de l'argent sur un échantillonnage inutile ou de détecter des différences non significatives sur le plan statistique.
Pour examiner plus en détail la relation entre l'effectif de l'échantillon et la différence (ou le rapport), pouvant être adaptée par le test à une puissance donnée, utilisez la courbe de puissance.
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -0,425 ou différence ≥ 0,425 |
| Hypothèse alternative : | -0,425 < différence < 0,425 |
| Niveau α : | 0,05 |
Résultats
| Différence | Effectif d'échantillon | Puissance cible | Puissance réelle |
|---|---|---|---|
| 0,0 | 2 | 0,9 | 0,978589 |
| 0,1 | 2 | 0,9 | 0,931544 |
| 0,2 | 3 | 0,9 | 0,972795 |
| 0,3 | 6 | 0,9 | 0,943646 |
| 0,4 | 107 | 0,9 | 0,900500 |
Ces résultats montrent que, lorsque l'importance de la différence augmente et qu'elle se rapproche de la valeur de la limite d'équivalence, vous avez besoin d'un effectif d'échantillon plus important pour atteindre la puissance donnée. Si la différence est de 0,1, seulement 2 participants sont nécessaires dans chaque séquence pour atteindre une puissance de 0,9. Si la différence est de 0,4, au moins 107 participants sont nécessaires dans chaque séquence pour atteindre une puissance de 0,9.
Puissance
La puissance d'un test d'équivalence constitue la probabilité que le test démontre que la différence se trouve dans vos limites d'équivalence lorsqu'elle l'est réellement. Elle dépend de l'effectif d'échantillon, de la différence, des limites d'équivalence, de la variabilité des données et du seuil de signification du test.
Pour plus d'informations, reportez-vous à la rubrique Puissance des tests d'équivalence.
Interprétation
Si vous indiquez un effectif d'échantillon et une différence (ou un rapport), Minitab calcule la puissance du test. Une valeur de puissance d'au moins 0,9 est généralement appropriée. Une puissance de 0,9 indique que vous avez 90 % de chances de démontrer une équivalence lorsque la différence (ou le rapport) entre les moyennes des populations se trouve réellement dans les limites d'équivalence. Si un test d'équivalence offre une faible puissance, il se peut que vous ne puissiez pas démontrer l'équivalence même lorsque la moyenne du test et la moyenne de référence sont équivalentes.
En général, plus l'effectif d'échantillon est faible ou plus la différence (ou le rapport) est proche d'une limite d'équivalence, moins le test est puissant pour établir une équivalence.
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -0,425 ou différence ≥ 0,425 |
| Hypothèse alternative : | -0,425 < différence < 0,425 |
| Niveau α : | 0,05 |
Résultats
| Différence | Effectif d'échantillon | Puissance |
|---|---|---|
| 0,3 | 8 | 0,984946 |
| 0,3 | 12 | 0,999089 |
| 0,4 | 8 | 0,189487 |
| 0,4 | 12 | 0,244815 |
Dans ces résultats, pour une différence de 0,3, la puissance du test est d'environ 0,98 avec un effectif d'échantillon de 8, et de 0,99 avec un effectif d'échantillon de 15. Pour une différence de 0,4, la puissance est d'environ 0,19 avec un effectif d'échantillon de 8, et de 0,24 avec un effectif d'échantillon de 12.
Courbe de la puissance
La courbe de puissance trace la puissance du test en fonction de la différence entre la moyenne du test et la moyenne de référence.
Interprétation
La courbe de puissance vous permet d'évaluer la puissance ou l'effectif d'échantillon adapté pour le test.
La courbe de puissance représente toutes les combinaisons de puissance et de différence (ou de rapport) pour chaque effectif de l'échantillon lorsque le seuil de signification et l'écart type (ou le coefficient de variation) restent constants. Chaque symbole sur la courbe de puissance représente une valeur calculée en fonction des valeurs saisies. Par exemple, si vous entrez un effectif d'échantillon et une valeur de puissance, Minitab calcule la différence (ou le rapport) correspondante et affiche la valeur calculée sur le graphique.
Examinez les valeurs sur la courbe pour déterminer la différence (ou le rapport) entre la moyenne du test et la moyenne de référence, pouvant être adaptée à une valeur de puissance et un effectif d'échantillon spécifiques. La valeur de puissance 0,9 est généralement appropriée. Toutefois, certains spécialistes considèrent que la valeur 0,8 est adéquate. Si un test d'équivalence offre une puissance inférieure, il se peut que vous ne puissiez pas démontrer l'équivalence même lorsque les moyennes de population sont équivalentes. Si vous augmentez l'effectif de l'échantillon, la puissance du test augmente également. L'échantillon doit contenir suffisamment d'observations pour atteindre une puissance adéquate. Toutefois, si l'effectif de l'échantillon est trop grand, vous risquez de gaspiller du temps et de l'argent sur un échantillonnage inutile ou de détecter des différences non significatives sur le plan statistique. Dans la plupart des cas, les différences (ou les rapports) plus proches des limites d'équivalence requièrent une puissance plus importante pour démontrer l'équivalence.
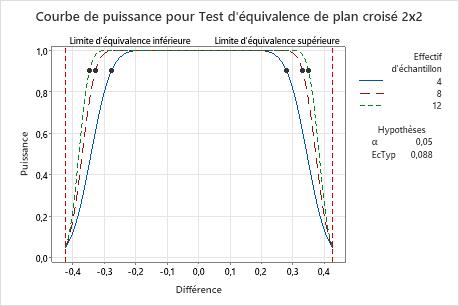
Dans ce graphique, les courbes de puissance pour tous les effectifs d'échantillons indiquent que le test offre une puissance adéquate (≥ 0,9) pour une différence d'environ ±0,25. Les effectifs d'échantillons représentent le nombre de participants dans chaque séquence. La courbe de puissance pour un effectif d'échantillon de 4 indique que le test offre une puissance de 0,9 pour une différence d'approximativement ±0,28. La courbe de puissance pour un effectif d'échantillon de 12 indique que le test offre une puissance de 0,9 pour une différence d'approximativement ±0,33. Notez que l'augmentation de l'effectif d'échantillon jusqu'à 12 n'augmente que très peu la différence pouvant être adaptée à une puissance de 0,9. Pour chaque courbe, lorsque la différence se rapproche de la limite d'équivalence inférieure ou supérieure, la puissance du test diminue et se rapproche de α (alpha, qui représente le risque de déclarer l'équivalence alors qu'elle n'existe pas).
