Etape 1 : examiner les valeurs calculées
- Différence (ou rapport)
- Si vous entrez l'effectif de l'échantillon et la puissance du test, Minitab calcule la différence (ou le rapport) pouvant être adaptée par le test à la puissance et à l'effectif d'échantillon indiqués. Pour des effectifs d'échantillons plus grands, la différence (ou le rapport) peut être plus proche des limites d'équivalence. Cette valeur représente la différence (ou le rapport) entre la moyenne de la population de test et la moyenne de la population de référence.
- Effectif d'échantillon
- Si vous indiquez une différence (ou un rapport) et une valeur de puissance pour le test, Minitab calcule l'effectif d'échantillon nécessaire. Si vous augmentez l'effectif de l'échantillon, la puissance du test augmente également. L'échantillon doit contenir suffisamment d'observations pour atteindre une puissance adéquate. Toutefois, si l'effectif de l'échantillon est trop grand, vous risquez de gaspiller du temps et de l'argent sur un échantillonnage inutile ou de détecter des différences non significatives sur le plan statistique.
Remarque
Etant donné que les effectifs d'échantillons sont des nombres entiers, la puissance réelle du test peut être légèrement supérieure à la valeur de puissance que vous avez indiquée.
- Puissance
- Si vous indiquez un effectif d'échantillon et une différence (ou un rapport), Minitab calcule la puissance du test. Une valeur de puissance d'au moins 0,9 est généralement appropriée. Une puissance de 0,9 indique que vous avez 90 % de chances de démontrer une équivalence lorsque la différence (ou le rapport) entre les moyennes des populations se trouve réellement dans les limites d'équivalence. Si un test d'équivalence offre une faible puissance, il se peut que vous ne puissiez pas démontrer l'équivalence même lorsque la moyenne du test et la moyenne de référence sont équivalentes.En général, plus l'effectif d'échantillon est faible ou plus la différence (ou le rapport) est proche d'une limite d'équivalence, moins le test est puissant pour établir une équivalence.
Remarque
Les définitions et l'interprétation dans cette rubrique sont applicables à un test d'équivalence utilisant l'hypothèse alternative par défaut pour la différence (Limite inférieure < moyenne du test - moyenne de référence < limite supérieure) ou l'hypothèse alternative par défaut pour le rapport (Limite inférieure < moyenne du test / moyenne de référence < limite supérieure).
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -1 ou différence ≥ 1 |
| Hypothèse alternative : | -1 < différence < 1 |
| Niveau α : | 0,05 |
| Ecart type supposé : | 0,31 |
Résultats
| Différence | Effectif d'échantillon | Puissance |
|---|---|---|
| 0,8 | 25 | 0,727010 |
Résultats principaux : différence, effectif de l'échantillon et puissance
Ces résultats montrent que si l'effectif de l'échantillon est de 25 dans chaque groupe et que la différence est de 0,8, la puissance du test pour démontrer l'équivalence est d'environ 0,73. Etant donné que la puissance du test n'est pas adéquate pour une différence de 0,8, vous devez augmenter l'effectif de l'échantillon, si possible. Vous pouvez également utiliser la courbe de puissance pour déterminer à quelle valeur de différence plus petite le test peut atteindre la puissance adéquate (0,9) avec l'effectif d'échantillon donné.
Etape 2 : examiner la courbe de puissance
La courbe de puissance vous permet d'évaluer la puissance ou l'effectif d'échantillon adapté pour le test.
La courbe de puissance représente toutes les combinaisons de puissance et de différence (ou de rapport) pour chaque effectif de l'échantillon lorsque le seuil de signification et l'écart type (ou le coefficient de variation) restent constants. Chaque symbole sur la courbe de puissance représente une valeur calculée en fonction des valeurs saisies. Par exemple, si vous entrez un effectif d'échantillon et une valeur de puissance, Minitab calcule la différence (ou le rapport) correspondante et affiche la valeur calculée sur le graphique.
Examinez les valeurs sur la courbe pour déterminer la différence (ou le rapport) entre la moyenne du test et la moyenne de référence, pouvant être adaptée à une valeur de puissance et un effectif d'échantillon spécifiques. La valeur de puissance 0,9 est généralement appropriée. Toutefois, certains spécialistes considèrent que la valeur 0,8 est adéquate. Si un test d'équivalence offre une puissance inférieure, il se peut que vous ne puissiez pas démontrer l'équivalence même lorsque les moyennes de population sont équivalentes. Si vous augmentez l'effectif de l'échantillon, la puissance du test augmente également. L'échantillon doit contenir suffisamment d'observations pour atteindre une puissance adéquate. Toutefois, si l'effectif de l'échantillon est trop grand, vous risquez de gaspiller du temps et de l'argent sur un échantillonnage inutile ou de détecter des différences non significatives sur le plan statistique. Dans la plupart des cas, les différences (ou les rapports) plus proches des limites d'équivalence requièrent une puissance plus importante pour démontrer l'équivalence.
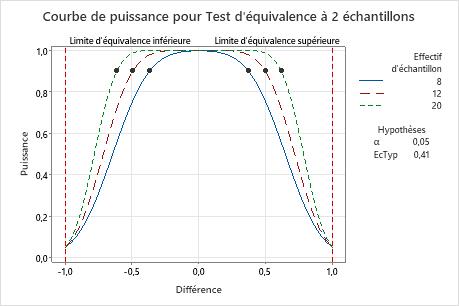
Dans ce graphique, la courbe de puissance pour un effectif d'échantillon de 8 (dans chaque groupe) indique que le test offre une puissance de 0,9 pour une différence d'approximativement ±0,4. La courbe de puissance pour un effectif d'échantillon de 12 indique que le test offre une puissance de 0,9 pour une différence d'approximativement ±0,5. La courbe de puissance pour un effectif d'échantillon de 12 indique que le test offre une puissance de 0,9 pour une différence d'approximativement ±0,6. Pour chaque courbe, lorsque la différence se rapproche de la limite d'équivalence inférieure ou supérieure, la puissance du test diminue et se rapproche de α (alpha, qui représente le risque de déclarer l'équivalence alors qu'elle n'existe pas).
