Un analyste de la qualité veut déterminer si la quantité moyenne d'ingrédient actif dans un analgésique d'une marque générique est à 1 mg près de celle d'un analgésique d'une marque populaire. Avant de collecter les données pour un test d'équivalence à 2 échantillons, l'analyste utilise un calcul de puissance et d'effectif d'échantillon afin de déterminer l'effectif d'échantillon nécessaire pour obtenir une puissance de 90 % (0,9). En se fondant sur des échantillons précédents, il estime l'écart type de la population à 0,41.
- Sélectionnez .
- Dans la fonction Hypothèse sur, sélectionnez Moyenne du test - moyenne de référence (différence).
- Dans la fonction Que souhaitez-vous déterminer ? (Hypothèse alternative), sélectionnez Limite inférieure < moyenne du test - moyenne de référence < limite supérieure.
- Dans la zone Limite inférieure, saisissez -1. Dans la zone Limite supérieure, saisissez 1.
- Dans la zone Différences (dans les limites), saisissez 0,5 0,7 0,9.
- Dans la zone Valeurs de puissance, saisissez 0,9.
- Dans la zone Ecart type, saisissez 0,41.
- Cliquez sur OK.
Interprétation des résultats
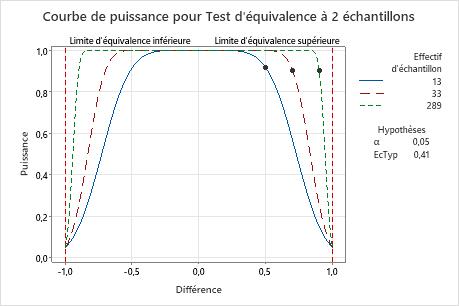
Si la différence est de 0,5, 13 observations sont nécessaires dans chaque groupe pour atteindre une puissance de 0,9. Si l'analyste utilise un effectif d'échantillon de 13, la puissance du test est d'approximativement 0,92.
Lorsque la différence est plus proche de la limite d'équivalence inférieure (–1) ou de la limite d'équivalence supérieure (1), l'analyste a besoin d'un effectif d'échantillon plus important pour atteindre la même puissance. Par exemple, pour une différence de 0,9, l'analyste a besoin d'un effectif d'échantillon d'au moins 289 observations dans chaque groupe pour atteindre la puissance de 0,9.
Pour tout effectif d'échantillon, lorsque la différence se rapproche de la limite d'équivalence inférieure ou supérieure, la puissance du test diminue et se rapproche de α (alpha, qui représente le risque de déclarer l'équivalence alors qu'elle n'existe pas).
Méthode
| Puissance pour la différence : | Moyenne du test - moyenne de référence |
|---|---|
| Hypothèse nulle : | Différence ≤ -1 ou différence ≥ 1 |
| Hypothèse alternative : | -1 < différence < 1 |
| Niveau α : | 0,05 |
| Ecart type supposé : | 0,41 |
Résultats
| Différence | Effectif d'échantillon | Puissance cible | Puissance réelle |
|---|---|---|---|
| 0,5 | 13 | 0,9 | 0,915407 |
| 0,7 | 33 | 0,9 | 0,902461 |
| 0,9 | 289 | 0,9 | 0,900360 |