Méthodes et formules pour Puissance et effectif de l'échantillon pour un test d'équivalence à 1 échantillon

Puissance

Soit t_α,v la valeur critique (unilatérale) α supérieure pour une loi T avec v degrés de liberté. La puissance pour l'hypothèse alternative bilatérale Limite inférieure < moyenne du test - cible < limite supérieure est exprimée de la façon suivante :

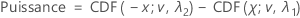
Pour l'hypothèse alternative de Moyenne du test > cible ou Moyenne du test - cible > limite inférieure, la puissance est exprimée de la façon suivante :

Pour l'hypothèse alternative de Moyenne du test < cible ou Moyenne du test - cible < limite supérieure, la puissance est exprimée de la façon suivante :

où la CDF (x ; v, λ) est la fonction de répartition, évaluée à x, pour une loi T non centrale avec le paramètre de non-centralité λ et v degrés de liberté.

Degrés de liberté

Les degrés de liberté, v, sont exprimés de la façon suivante :

Paramètres de non-centralité

Le paramètre de non-centralité correspondant à la limite d'équivalence inférieure est dénoté par λ₁ et exprimé de la façon suivante :

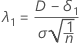
Pour l'hypothèse alternative de Moyenne du test > cible, δ₁ = 0.

Le paramètre de non-centralité correspondant à la limite d'équivalence supérieure est dénoté par λ₂ et exprimé de la façon suivante :

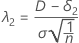
Pour l'hypothèse alternative de Moyenne du test < cible, δ₂ = 0.

Notation

Terme	Description
α	seuil de signification pour le test
D	moyenne de la population du test moins la valeur cible
δ1	limite d'équivalence inférieure
δ2	limite d'équivalence supérieure
n	effectif d'échantillon
σ	écart type d'une population

Si vous indiquez les valeurs de la puissance et de la différence, Minitab calcule l'effectif de l'échantillon. Minitab utilise la formule de puissance appropriée et un algorithme itératif afin d'identifier le plus petit effectif de l'échantillon, n, pour lequel la puissance est supérieure ou égale à la valeur spécifiée. La puissance réelle pour n est susceptible d'être supérieure à la puissance indiquée. Cela est dû au fait que n doit être une valeur d'entier discrète et qu'aucune valeur n n'est susceptible de générer exactement la valeur de puissance spécifiée.

Si vous indiquez les valeurs de la puissance et de l'effectif de l'échantillon, Minitab calcule les valeurs de la différence. Minitab utilise la formule de puissance appropriée et un algorithme itératif afin d'identifier la plus petite et/ou la plus grande différence pour laquelle la puissance est supérieure ou égale à la valeur spécifiée.