Rang moyen
- Il classe les valeurs des échantillons combinés dans l'ordre, en attribuant le rang 1 à la plus petite observation, le rang 2 à la deuxième plus petite observation, et ainsi de suite.
- Si deux observations ou plus sont égales, Minitab leur attribue la moyenne de leurs rangs respectifs.
- Il calcule la moyenne des rangs de chaque échantillon.
Minitab affiche les valeurs de chaque groupe sous Rang moyen dans les résultats.
Valeur de Z
Formule
Minitab calcule la valeur de Z de chaque groupe comme suit :
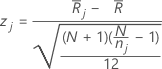
Notation
| Terme | Description |
|---|---|
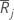 | rang moyen du groupe j |
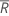 | rang moyen de toutes les observations |
| N | Nombre d'observations. |
| nj | nombre d'observations dans le je groupe |
Classement des valeurs ex aequo
- Il classe les observations par ordre croissant.
- Il attribue un rang à chaque observation comme s'il n'existait aucune valeur ex aequo.
- Pour tout ensemble de valeurs ex aequo, il prend la moyenne des rangs correspondants et attribue cette valeur comme nouveau rang à toutes les valeurs ex aequo de cet ensemble.
Exemple
Un échantillon comporte 9 observations : 2,4 ; 5,3 ; 2,4 ; 4,0 ; 1,2 ; 3,6 ; 4,0 ; 4,3 et 4,0
| Observation | Rang (sans valeurs ex aequo) | Rang |
|---|---|---|
| 1,2 | 1 | 1 |
| 2,4 | 2 | 2,5 |
| 2,4 | 3 | 2,5 |
| 3,6 | 4 | 4 |
| 4,0 | 5 | 6 |
| 4,0 | 6 | 6 |
| 4,0 | 7 | 6 |
| 4,3 | 8 | 8 |
| 5,3 | 9 | 9 |
- Nombre d'ensembles de valeurs ex aequo = 2
- Nombre de valeurs ex aequo dans le premier ensemble = 2
- Nombre de valeurs ex aequo dans le second ensemble = 3
H
Formule

Sous l'hypothèse nulle, la loi du Khi deux avec k – 1 degrés de liberté offre une approximation de la loi de distribution de H. Cette approximation est raisonnablement précise quand aucun groupe ne comporte moins de cinq observations. Plus la valeur de H est élevée, plus vous pouvez accepter l'hypothèse nulle selon laquelle la différence entre certaines médianes est statistiquement significative.
Certains auteurs, comme Lehmann (1975)1, suggèrent d'ajuster H lorsque les données comportent des valeurs ex aequo. Minitab affiche H(ajust) lorsque les données comportent des valeurs ex aequo.
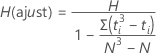
Sous l'hypothèse nulle, la loi du Khi deux avec k – 1 degrés de liberté offre une approximation de la loi de distribution de H et de H(ajust).
Valeur de p = 1 – CDF (χ2H, df)
Valeur de p = 1 – CDF (χ2H(ajust), df)
Pour les petits échantillons, Minitab vous recommande d'utiliser des tableaux exacts. Pour plus de détails, reportez-vous à Hollander et Wolfe (1973)2.
Notation
| Terme | Description |
|---|---|
| nj | nombre d'observations dans le groupe j |
| N | effectif total de l'échantillon |
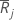 | moyenne des rangs du groupe j |
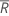 | moyenne de tous les rangs |
| ti | nombre de valeurs ex aequo dans le ie ensemble de valeurs ex aequo |
