Sur ce thème
S
La statistique de test obéit approximativement à une loi du Khi deux ( χ2), avec (k – 1) degrés de liberté. Si les données d'un ou de plusieurs blocs contiennent des valeurs ex aequo, Minitab utilise le rang moyen et affiche une statistique de test corrigée pour les valeurs ex aequo. Pour plus de détails sur cette méthode, reportez-vous à M. Hollander et D.A. Wolfe (1973)1.
Formule
Pour calculer la statistique de test pour une loi du Khi deux, Minitab classe les données de chaque bloc séparément et additionne les rangs pour chaque traitement.
Si les données ne contiennent pas de valeurs ex aequo, la formule est la suivante :
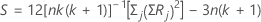
Si les données contiennent des valeurs ex aequo, la formule est la suivante :

où C est un facteur de correction égal à :
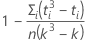
Notation
| Terme | Description |
|---|---|
| j | 1, 2, ..., k |
| k | nombre de conditions de traitement |
| n | nombre de blocs |
| Rj | somme des rangs pour le traitement j |
| i | 1, 2, ..., m |
| m | nombre d'ensembles de valeurs ex aequo |
| ti | nombre de scores ex aequo dans le ie ensemble de valeurs ex aequo |
- M. Hollander et D.A. Wolfe (1973), Nonparametric Statistical Methods, John Wiley & Sons, Inc.
Grande médiane
Pour comprendre comment calculer les effets des traitements, les médianes de bloc et la grande médiane, étudiez les données ci-dessous.
| Bloc | ||||
| Traitement | 1 | 2 | 3 | 4 |
| 1 | 0,15 | 0,26 | 0,23 | 0,99 |
| 2 | 0,55 | 0,26 | −0,22 | 0,99 |
| 3 | 0,55 | 0,66 | 0,77 | 0,99 |
Pour calculer les effets des traitements (méthode de Doksum1), commencez par déterminer la différence médiane entre des paires de traitements. Les différence deux à deux pour Traitement 1 – Traitement 2 sont 0,15 – 0,55 = −0,4 ; 0,26 – 0,26 = 0 ; 0,23 – (−0,22) = 0,45 et 0,99 – 0,99 = 0. La médiane des différences est 0. Ce calcul fournit une différence médiane de −0,4 pour Traitement 1 – Traitement 3 et −0,2 pour Traitement 2 – Traitement 3.
L'effet de chaque traitement est la moyenne des différences médianes entre ce traitement et tous les autres (y compris lui-même). Pour les données de cet exemple, effet(2) = [médiane (2 – 1) + médiane (2 – 2) + médiane (2 – 3)]/3 = (0,00 + 0,00 – 0,20)/3 = −0,0667. De la même façon, effet(1) = −0,1333 et effet(3) = 0,20.
Pour calculer les médianes de bloc ajustées, vous devez ajuster chaque observation en y soustrayant l'effet de traitement correspondant. Les médianes de bloc ajustées sont simplement les médianes de ces données ajustées, calculées pour chaque bloc. La grande médiane est la médiane des médianes de bloc ajustées. La médiane estimée pour chaque niveau de traitement est égale à la grande médiane plus l'effet du traitement.
- M. Hollander et D.A. Wolfe (1973), Nonparametric Statistical Methods, John Wiley & Sons, Inc., pp. 158-161.
Classement des valeurs ex aequo
- Il classe les observations par ordre croissant.
- Il attribue un rang à chaque observation comme s'il n'existait aucune valeur ex aequo.
- Pour tout ensemble de valeurs ex aequo, il prend la moyenne des rangs correspondants et attribue cette valeur comme nouveau rang à toutes les valeurs ex aequo de cet ensemble.
Exemple
Un échantillon comporte 9 observations : 2,4 ; 5,3 ; 2,4 ; 4,0 ; 1,2 ; 3,6 ; 4,0 ; 4,3 et 4,0
| Observation | Rang (sans valeurs ex aequo) | Rang |
|---|---|---|
| 1,2 | 1 | 1 |
| 2,4 | 2 | 2,5 |
| 2,4 | 3 | 2,5 |
| 3,6 | 4 | 4 |
| 4,0 | 5 | 6 |
| 4,0 | 6 | 6 |
| 4,0 | 7 | 6 |
| 4,3 | 8 | 8 |
| 5,3 | 9 | 9 |
- Nombre d'ensembles de valeurs ex aequo = 2
- Nombre de valeurs ex aequo dans le premier ensemble = 2
- Nombre de valeurs ex aequo dans le second ensemble = 3
