Sur ce thème
Etape 1 : Déterminer si la moyenne de test et la moyenne de référence sont équivalentes
Comparez l'intervalle de confiance aux limites d'équivalence. Si l'intervalle de confiance se trouve entièrement entre les limites d'équivalence, vous pouvez affirmer que la moyenne de la population de test est équivalente à la moyenne de la population de référence. Si une partie de l'intervalle de confiance se trouve en dehors des limites d'équivalence, vous ne pouvez pas affirmer qu'il existe une équivalence.
Différence : moyenne(Nouvelle) - moyenne(Marque phare)
| Différence | EcTyp | ErT | IC 95% pour équivalence | Intervalle d'équivalence |
|---|---|---|---|---|
| -0,11929 | 0,42324 | 0,11312 | (-0,319605; 0,0810335) | (-0,5; 0,5) |
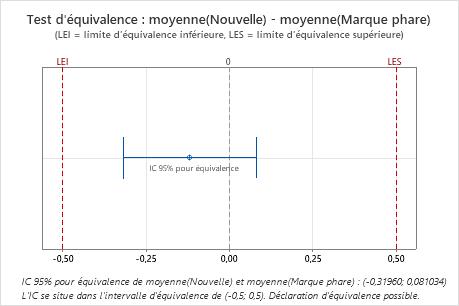
Résultats principaux : IC à 95 %, intervalle d'équivalence
Dans ces résultats, l'intervalle de confiance à 95 % est entièrement compris dans l'intervalle défini par les limites d'équivalence inférieure (LEI) et supérieure (LES). Vous pouvez donc en conclure que la moyenne de test équivaut à la moyenne de référence.
Remarque
Vous pouvez également utiliser les valeurs de p pour évaluer les résultats du test d'équivalence. Pour démontrer l'équivalence, les valeurs de p des deux hypothèses nulles doivent être inférieures à alpha.
Etape 2 : rechercher les problèmes dans les données
Certains problèmes avec les données, comme la présence d'une asymétrie ou de valeurs aberrantes, risquent de nuire à vos résultats. Utilisez les graphiques pour rechercher toute asymétrie (en examinant la dispersion des données) et pour détecter d'éventuelles valeurs aberrantes.
Déterminer si les données sont asymétriques
Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à identifier avec un histogramme ou une boîte à moustaches.
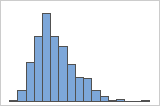
Asymétrie à droite
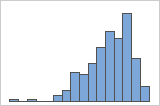
Asymétrie vers la gauche
Par exemple, l'histogramme avec des données asymétriques à droite illustre des données salariales. De nombreux employés reçoivent un salaire relativement faible et de moins en moins d'employés reçoivent un salaire élevé. L'histogramme avec des données asymétriques à gauche représente des données de taux de défaillance. Quelques éléments rencontrent une défaillance tôt, tandis que pour un nombre croissant d'entre eux, la défaillance survient plus tard.
Les données très asymétriques peuvent avoir une incidence sur la validité des résultats de test si votre échantillon est petit (moins de 20 valeurs). Si vos données sont très asymétriques et que vous avez un petit échantillon, pensez éventuellement à augmenter l'effectif d'échantillon.
Identification des valeurs aberrantes
Les valeurs aberrantes, qui sont des points de données très éloignés de la majorité des autres données, peuvent avoir une incidence importante sur les résultats. Elles sont plus faciles à repérer sur une boîte à moustaches.
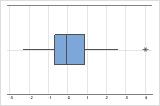
Sur une boîte à moustaches, les valeurs aberrantes sont indiquées par des astérisques (*).
Sur le diagramme de profil du sujet, recherchez une réponse de sujet qui diffère largement des autres réponses et des résultats de test d'équivalence.
Vous devez essayer de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez les données associées à des causes spéciales et procédez à une nouvelle analyse. Pour plus d'informations sur les causes spéciales, reportez-vous à la rubrique Utilisation des cartes de contrôle pour détecter une variation due à des causes communes et une variation due à des causes spéciales.
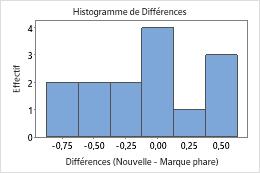
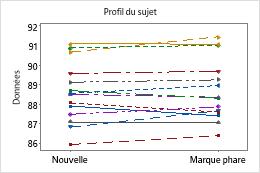
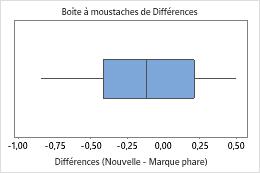
La boîte à moustaches et l'histogramme indiquent que les différences ne sont pas asymétriques et qu'il n'existe aucune valeur aberrante. Le diagramme de profil du sujet indique que les mesures peuvent varier d'un participant à l'autre. Toutefois, les lignes reliant chaque paire d'observations sont presque horizontales. De ce fait, les valeurs pour le traitement de test et le traitement de référence sont similaires pour chaque sujet. Ce schéma est cohérent avec les résultats statistiques suggérant que les deux solutions sont aussi efficaces l'une que l'autre.
