Méthodes et formules pour les concepts communs utilisés dans la fonction est d'équivalence pour plan croisé 2x2

L'ensemble des calculs du test d'équivalence pour le plan croisé 2x2 supposent que l'ordre des traitements dans la séquence 1 est Traitement de référence puis Traitement de test, et que l'ordre de la séquence 2 est Traitement de test puis Traitement de référence.

Soit Y_ijk la réponse pour le participant k lors de la période j dans la séquence i, où i = 1, 2 ; j = 1, 2 ; k = 1 ... n_i .

Si la réponse pour l'une des périodes est manquante pour un participant, les données de ce participant sont omises dans les calculs.

Soit d_1k et d_2k deux valeurs définies comme suit :

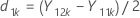
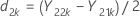
Soit et S₁ la moyenne de l'échantillon et l'écart type de l'échantillon pour d_1k, k = 1, ..., n₁, calculé comme suit :

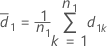
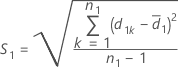
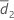Soit et S₂ la moyenne de l'échantillon et l'écart type de l'échantillon pour d_2k, k = 1, ..., n₂, calculé comme suit :

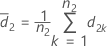
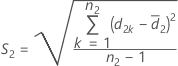
Notation

Terme	Description
	Moyenne de l'échantillon pour d1k, k = 1, ..., n1
S1	Ecart type de l'échantillon pour d1k, k = 1, ..., n1
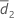	Moyenne de l'échantillon pour d2k, k = 1, ..., n2
S2	Ecart type de l'échantillon pour d2k, k = 1, ..., n2

Notation

Terme	Description
ν	Degrés de liberté
n  1	Nombre de participants dans la séquence 1
n  2	Nombre de participants dans la séquence 2

Soit k₁ la limite inférieure que vous specifiez et k₂ la limite supérieure. Par défaut, la limite d'équivalence inférieure, δ₁, est calculée de la façon suivante :

et la limite d'équivalence supérieure, δ₂, de la façon suivante :

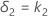
Toutefois, si vous sélectionnez l'option permettant de multiplier vos limites par la moyenne de référence, 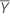, les limites sont obtenues de la façon suivante :

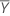est la moyenne des réponses moyennes pour les deux périodes de référence.