Interprétation des résultats principaux pour la fonction est d'équivalence pour plan croisé 2x2

Effectuez les étapes suivantes pour interpréter un test d'équivalence pour plan croisé 2x2. Les résultats principaux incluent les estimations des effets, leurs valeurs de p, les estimations de la différence (ou du rapport), l'intervalle de confiance, le diagramme d'équivalence et d'autres graphiques.

Sur ce thème

Etape 1 : Rechercher les effets potentiels de rémanence ou de période
Etape 2 : Déterminer si la moyenne de test et la moyenne de référence sont équivalentes

Etape 1 : Rechercher les effets potentiels de rémanence ou de période

Un effet de rémanence significatif indique que le traitement administré durant la première période peut affecter la réponse à l'autre traitement administré durant la deuxième période. Un effet de période significatif indique que la période d'administration du traitement peut affecter la réponse au traitement.

Important

Si l'effet de rémanence ou de période est significatif sur le plan statistique, vous ne pouvez pas déterminer l'équivalence car les résultats peuvent être biaisés par ces effets.

Utilisez la valeur de p pour chaque effet afin de déterminer s'il est statistiquement significatif. Si la valeur de p pour un effet est inférieure au niveau d'alpha (généralement 0,05), l'effet est significatif.

Effets

	Effet	ErT	DL	Valeur de T	Valeur de P	IC 95% pour équivalence
Rémanence	0,45181	0,64988	15	0,69521	0,498	(-0,93339; 1,8370)
Traitement	-0,32104	0,060641	15	-5,2941	0,000	(-0,45030; -0,19179)
Période	-0,097708	0,060641	15	-1,6112	0,128	(-0,22696; 0,031546)

Résultats principaux : valeurs de p pour les effets

Dans ces résultats, la valeur de p pour l'effet de rémanence (0,498) et la valeur de p pour l'effet de période (0,128) sont supérieures à 0,05. Ces effets ne sont donc pas significatifs au niveau 0,05.

Etape 2 : Déterminer si la moyenne de test et la moyenne de référence sont équivalentes

Comparez l'intervalle de confiance aux limites d'équivalence. Si l'intervalle de confiance se trouve entièrement entre les limites d'équivalence, vous pouvez affirmer que la moyenne de la population de test est équivalente à la moyenne de la population de référence. Si une partie de l'intervalle de confiance se trouve en dehors des limites d'équivalence, vous ne pouvez pas affirmer qu'il existe une équivalence.

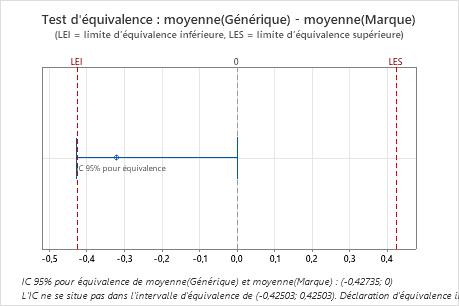
Résultats principaux : IC à 95 %, intervalle d'équivalence

Dans ces résultats, l'intervalle de confiance à 95 % ne se trouve pas complètement dans l'intervalle d'équivalence défini par les limites d'équivalence inférieure (LEI) et supérieure (LES). La borne inférieure de l'intervalle de confiance se prolonge au-delà de la limite d'équivalence inférieure. Vous ne pouvez donc pas en conclure que la moyenne de test équivaut à la moyenne de référence.