Sur ce thème
Rapport
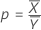
Notation
| Terme | Description |
|---|---|
| ρ | Rapport |
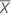 | Moyenne du test |
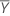 | Moyenne de référence |
Moyennes et écarts types
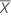 , est obtenue de la façon suivante :
, est obtenue de la façon suivante :
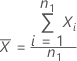
La moyenne de l'échantillon de référence, 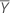 , est obtenue de la façon suivante :
, est obtenue de la façon suivante :
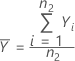
L'écart type de l'échantillon de test, S1, est obtenu de la façon suivante :
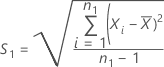
L'écart type de l'échantillon de référence, S2, est obtenu de la façon suivante :
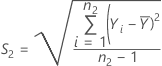
Notation
| Terme | Description |
|---|---|
| X i | Observations de l'échantillon de test, avec i = 1, ..., n1 |
| Y i | Observations de l'échantillon de référence, avec i = 1, ..., n2 |
| n 1 | Nombre d'observations dans l'échantillon de test |
| n 2 | Nombre d'observations dans l'échantillon de référence |
Limite d'équivalence
Soit k1 la valeur indiquée pour la limite inférieure et k2 la valeur indiquée pour la limite supérieure. Par défaut, la limite d'équivalence inférieure, δ1, est indiquée par :

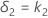
et la limite d'équivalence supérieure δ2, est indiquée par :
Degrés de liberté (DL)
Ne pas supposer des variances égales (par défaut)
Par défaut, les degrés de liberté pour le test, v, sont obtenus avec la formule suivante :
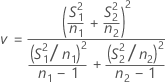
Minitab arrondit v à l'entier inférieur.
Supposer des variances égales
Si vous sélectionnez l'option Supposer les variances égales, Minitab calcule les degrés de liberté de la façon suivante :

Notation
| Terme | Description |
|---|---|
| S1 | Ecart type de l'échantillon de test |
| n 1 | Nombre d'observations dans l'échantillon de test |
| S2 | Ecart type de l'échantillon de référence |
| n 2 | Nombre d'observations dans l'échantillon de référence |
Ecart type regroupé
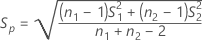
Notation
| Terme | Description |
|---|---|
| Sp | Ecart type regroupé |
| S1 | Ecart type de l'échantillon de test |
| n 1 | Nombre d'observations dans l'échantillon de test |
| S2 | Ecart type de l'échantillon de référence |
| n 2 | Nombre d'observations dans l'échantillon de référence |
Intervalle de confiance
Minitab ne peut pas calculer l'intervalle de confiance (IC) si l'une des trois conditions suivantes n'est pas remplie :

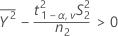
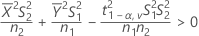
Ne pas supposer des variances égales (par défaut)
- IC à 100(1 - α) %
Par défaut, Minitab calcule l'IC à 100(1 - α) % pour ρ de la façon suivante :
IC = [min(C, ρI), max(C, ρS)]
où :
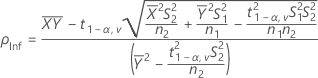
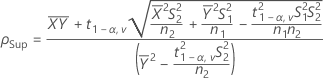
- IC à 100(1 - 2α) %
Si vous sélectionnez l'option qui utilise un IC à 100(1 - 2α) %, l'IC est obtenu de la façon suivante :
IC = [ρI, ρS]
Supposer des variances égales
Si vous sélectionnez l'option Supposer les variances égales, l'IC est calculé de la façon suivante :
Minitab ne peut pas calculer l'IC si l'une des trois conditions suivantes n'est pas remplie :

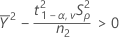
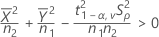
- IC à 100(1 - α) %
Minitab calcule l'IC à 100(1 - α) % de la façon suivante :
IC = [min(C, ρI), max(C, ρS)]
où :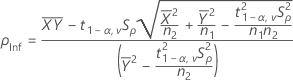
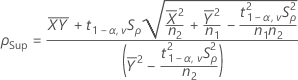
- IC à 100(1 - 2α) %
Si vous sélectionnez l'option qui utilise un IC à 100(1 - 2α) %, l'IC est obtenu de la façon suivante :
IC = (ρI, ρS)
Intervalles unilatéraux
Pour l'hypothèse Moyenne du test / moyenne de référence > limite inférieure, la borne inférieure à 100(1 - α) % est égale à ρI.
Pour l'hypothèse Moyenne du test / moyenne de référence < limite supérieure, la borne supérieure à 100(1 - α) % est égale à ρS.
Notation
| Terme | Description |
|---|---|
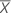 | Moyenne de l'échantillon de test |
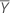 | Moyenne de l'échantillon de référence |
| S1 | Ecart type de l'échantillon de test |
| n 1 | Nombre d'observations dans l'échantillon de test |
| S2 | Ecart type de l'échantillon de référence |
| n 2 | Nombre d'observations dans l'échantillon de référence |
| δ1 | Limite d'équivalence inférieure |
| δ2 | Limite d'équivalence supérieure |
| Sρ | Ecart type regroupé |
| v | Degrés de liberté |
| α | Seuil de signification cible du test |
| t1-α,v | Valeur critique à 1 - α supérieure pour une loi t à v degrés de liberté |
Valeurs de t
Ne pas supposer des variances égales (par défaut)
Soit t1 la valeur de t pour l'hypothèse, , et soit t2 la valeur de t pour l'hypothèse,
, et soit t2 la valeur de t pour l'hypothèse,  , où Λ est le rapport entre la moyenne de la population de test et la
moyenne de la population de référence. Par défaut, les valeurs de t sont calculées comme
suit :
, où Λ est le rapport entre la moyenne de la population de test et la
moyenne de la population de référence. Par défaut, les valeurs de t sont calculées comme
suit : 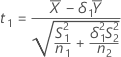
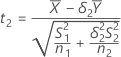
Supposer des variances égales
Si vous sélectionnez l'option permettant de supposer des variances égales, les valeurs de t sont calculées comme suit :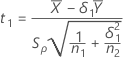
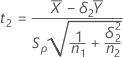
Notation
| Terme | Description |
|---|---|
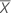 | Moyenne de l'échantillon de test |
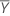 | Moyenne de l'échantillon de référence |
| S1 | Ecart type de l'échantillon de test |
| n 1 | Nombre d'observations dans l'échantillon de test |
| S2 | Ecart type de l'échantillon de référence |
| n 2 | Nombre d'observations dans l'échantillon de référence |
| Sρ | Ecart type regroupé |
| δ1 | Limite d'équivalence inférieure |
| δ2 | Limite d'équivalence supérieure |
Valeurs de p
Si  , alors :
, alors :
| H0 | valeur de p |
|---|---|
 |
 |
 |
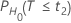 |
Notation
| Terme | Description |
|---|---|
| Λ | Rapport inconnu entre la moyenne de la population de test et la moyenne de la population de référence |
| δ1 | Limite d'équivalence inférieure |
| δ2 | Limite d'équivalence supérieure |
| v | Degrés de liberté |
| T | Loi T avec v degrés de liberté |
| t1 | Valeur de t pour l'hypothèse  |
| t2 | Valeur de t pour l'hypothèse  |
Remarque
Pour plus d'informations sur le calcul des valeurs de t, reportez-vous à la section sur les valeurs de t.
