Sur ce thème
Différence (D)
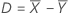
Notation
| Terme | Description |
|---|---|
| D | Différence |
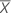 | Moyenne du test |
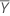 | Moyenne de référence |
Moyennes et écarts types
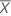 , est obtenue de la façon suivante :
, est obtenue de la façon suivante :
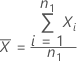
La moyenne de l'échantillon de référence, 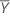 , est obtenue de la façon suivante :
, est obtenue de la façon suivante :
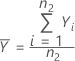
L'écart type de l'échantillon de test, S1, est obtenu de la façon suivante :
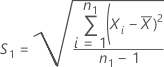
L'écart type de l'échantillon de référence, S2, est obtenu de la façon suivante :
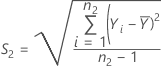
Notation
| Terme | Description |
|---|---|
| X i | Observations de l'échantillon de test, avec i = 1, ..., n1 |
| Y i | Observations de l'échantillon de référence, avec i = 1, ..., n2 |
| n 1 | Nombre d'observations dans l'échantillon de test |
| n 2 | Nombre d'observations dans l'échantillon de référence |
Erreur type de la différence (ErT)
Ne pas supposer des variances égales (par défaut)
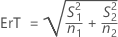
Supposer des variances égales
Si vous sélectionnez l'option Supposer les variances égales, Minitab calcule l'écart type regroupé, Sp, et l'erreur type de la différence, ErT, à l'aide des formules suivantes :
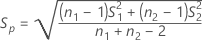
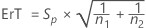
Notation
| Terme | Description |
|---|---|
| S1 | Ecart type de l'échantillon de test |
| n 1 | Nombre d'observations dans l'échantillon de test |
| S2 | Ecart type de l'échantillon de référence |
| n 2 | Nombre d'observations dans l'échantillon de référence |
| Sp | Ecart type regroupé |
Limite d'équivalence
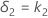
Soit k1 la valeur indiquée pour la limite inférieure et k2 la valeur indiquée pour la limite supérieure. Par défaut, la limite d'équivalence inférieure, δ1, est indiquée par :

et la limite d'équivalence supérieure δ2, est indiquée par :
Degrés de liberté (DL)
Ne pas supposer des variances égales (par défaut)
Par défaut, les degrés de liberté pour le test, v, sont obtenus avec la formule suivante :
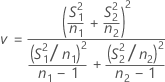
Minitab arrondit v à l'entier inférieur.
Supposer des variances égales
Si vous sélectionnez l'option Supposer les variances égales, Minitab calcule les degrés de liberté de la façon suivante :

Notation
| Terme | Description |
|---|---|
| S1 | Ecart type de l'échantillon de test |
| n 1 | Nombre d'observations dans l'échantillon de test |
| S2 | Ecart type de l'échantillon de référence |
| n 2 | Nombre d'observations dans l'échantillon de référence |
Intervalle de confiance
IC à 100(1-α) %
Par défaut, Minitab utilise la formule suivante pour calculer l'intervalle de confiance (IC) à 100(1 – α) % pour l'équivalence :
IC = [min(C, Di), max(C, Ds)]
où :

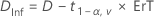
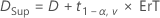
IC à 100(1-2α) %
Si vous sélectionnez l'option qui utilise un IC à 100(1 – 2α) %, l'IC est obtenu avec la formule suivante :
IC = [Di, Ds]
Intervalles unilatéraux
Pour les hypothèses Moyenne du test > moyenne de référence ou Moyenne du test - moyenne de référence > limite inférieure, la borne inférieure à 100(1 – α) % est égale à DI.
Pour l'hypothèse Moyenne du test < moyenne de référence ou Moyenne du test - moyenne de référence > limite supérieure, la borne supérieure à 100(1 – α) % est égale à DS.Notation
| Terme | Description |
|---|---|
| D | Différence entre la moyenne du test et la moyenne de référence |
| ErT | Erreur type |
| δ1 | Limite d'équivalence inférieure |
| δ2 | Limite d'équivalence supérieure |
| v | Degrés de liberté |
| α | Seuil de signification cible du test (alpha) |
| t1-α, v | Valeur critique à 1 – α supérieure pour une loi t à v degrés de liberté |
Valeurs de t
 , et soit t2 la valeur de t pour l'hypothèse,
, et soit t2 la valeur de t pour l'hypothèse,  , où
, où  est la différence entre la moyenne de la population de test et la moyenne de la population de référence. Par défaut, les valeurs de t sont calculées comme suit :
est la différence entre la moyenne de la population de test et la moyenne de la population de référence. Par défaut, les valeurs de t sont calculées comme suit :


Pour une hypothèse de Moyenne du test > moyenne de référence, δ1 = 0.
Pour une hypothèse de Moyenne du test < moyenne de référence, δ2 = 0.
Notation
| Terme | Description |
|---|---|
| D | Différence entre la moyenne du test de l'échantillon et la moyenne de référence de l'échantillon |
| SE | Erreur type de la différence |
| δ1 | Limite d'équivalence inférieure |
| δ2 | Limite d'équivalence supérieure |
Valeurs de p
| H0 | valeur de p |
|---|---|
 |
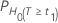 |
 |
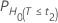 |
Notation
| Terme | Description |
|---|---|
 | Différence inconnue entre la moyenne de la population de test et celle de la population de référence. |
| δ1 | Limite d'équivalence inférieure |
| δ2 | Limite d'équivalence supérieure |
| v | Degrés de liberté |
| T | Loi t à v degrés de liberté |
| t1 | Valeur de t de l'hypothèse  |
| t2 | Valeur de t de l'hypothèse  |
Remarque
Pour plus d'informations sur le calcul des valeurs de t, reportez-vous à la section relative aux valeurs de t.
