Sur ce thème
Différence
Si vous sélectionnez une hypothèse sur la différence entre les moyennes, Minitab affiche la différence entre la moyenne du test et la moyenne de référence à partir des échantillons.
Interprétation
La moyenne de l'échantillon de test est une estimation de la moyenne de la population de test. La moyenne de l'échantillon de référence est une estimation de la moyenne de la population de référence. Par conséquent, la différence entre les moyennes d'échantillons fournit une estimation de la différence entre la moyenne de la population de test et la moyenne de la population de référence.
Puisque la différence est basée sur les données échantillons plutôt que sur l'ensemble des populations, vous ne pouvez pas être sûr qu'elle est égale à la différence entre la moyenne de la population de test et la moyenne de la population de référence. Pour évaluer la précision de l'estimation pour les populations, utilisez un intervalle de confiance.
Rapport
Si vous sélectionnez une hypothèse sur le rapport des moyennes, Minitab calcule le rapport de la moyenne du test et de la moyenne de l'échantillon de référence.
Interprétation
La moyenne de l'échantillon de test est une estimation de la moyenne de la population de test. La moyenne de l'échantillon de référence est une estimation de la moyenne de la population de référence. Par conséquent, le rapport des moyennes d'échantillons fournit une estimation du rapport de la moyenne de la population de test et de la moyenne de la population de référence.
Puisque le rapport est basé sur les données échantillons plutôt que sur l'ensemble des populations, vous ne pouvez pas être sûr qu'il est égal au rapport de population. Pour évaluer la précision de l'estimation pour les populations, utilisez un intervalle de confiance.
ErT
L'erreur type (ErT) de la différence estime la variabilité de la différence entre la moyenne du test et la moyenne de référence que vous obtiendriez si vous preniez des échantillons répétés des mêmes populations. L'erreur type de la différence évalue la variabilité d'un échantillon à un autre, tandis que l'écart type mesure la variabilité au sein d'un même échantillon.
Supposez, par exemple, une différence entre la moyenne de test de l'échantillon et la moyenne de référence de l'échantillon de −0,12122 unités. L'échantillon de test de 10 valeurs présente un écart type de 0,26138. L'échantillon de référence de 9 valeurs présente un écart type de 0,58064. L'erreur type de la différence est égale à la racine carrée de la somme (0,58064/10 + 0,26138/9), ou 0,20324. Si vous aviez collecté plusieurs échantillons aléatoires de même effectif et provenant de la même population, l'écart type des différences entre les échantillons tournerait autour de 0,20324.
Interprétation
Utilisez l'erreur type de la différence pour déterminer le degré de précision avec lequel la différence entre les moyennes d'échantillons permet d'estimer la différence entre la moyenne de la population de test et la moyenne de la population de référence.
Des valeurs moins élevées de l'erreur type indiquent une estimation plus précise. En règle générale, plus l'écart type est grand, plus l'erreur type de la différence sera élevée et moins l'estimation sera précise. En revanche, plus l'effectif d'échantillon est élevé, plus l'erreur type de la différence est faible et plus l'estimation est précise.
Minitab utilise l'erreur type de la différence pour calculer les statistiques du test (valeurs de t).
Intervalle de confiance (IC)
L'intervalle de confiance fournit une étendue de valeurs probables pour la différence (ou le rapport) entre la moyenne de la population de test et la moyenne de la population de référence. La limite de confiance inférieure définit une valeur à laquelle la différence (ou le rapport) est susceptible d'être supérieure. La limite de confiance supérieure définit une valeur à laquelle la différence (ou le rapport) est susceptible d'être inférieure.
Remarque
Si vous effectuez un test d'équivalence avec les paramètres par défaut, Minitab affiche un intervalle de confiance pour l'équivalence. Si vous modifiez les paramètres par défaut et utilisez la méthode alternative pour calculer l'intervalle de confiance, Minitab affiche un intervalle de confiance type. Pour obtenir des informations sur la différence entre ces intervalles, renseignez-vous sur les intervalles de confiance dans le test d'équivalence.
Interprétation
Comparez l'intervalle de confiance aux limites d'équivalence. Si l'intervalle de confiance se trouve entièrement entre les limites d'équivalence, vous pouvez affirmer que la moyenne de la population de test est équivalente à la moyenne de la population de référence. Si une partie de l'intervalle de confiance se trouve en dehors des limites d'équivalence, vous ne pouvez pas affirmer qu'il existe une équivalence.
Différence : moyenne(Prix réduit) - moyenne(Original)
| Différence | ErT | IC 95% pour équivalence | Intervalle d'équivalence |
|---|---|---|---|
| -0,12122 | 0,20324 | (-0,483449; 0,241005) | (-0,5; 0,5) |
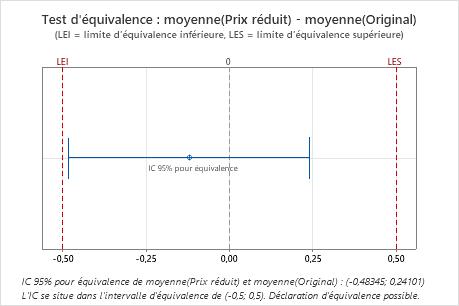
Dans ces résultats, l'intervalle de confiance à 95 % se trouve complètement dans l'intervalle d'équivalence défini par les limites d'équivalence inférieure (LEI) et supérieure (LES). Vous pouvez donc en conclure que la moyenne de test équivaut à la moyenne de référence.
Intervalle d'équivalence
Un intervalle d'équivalence est une étendue de valeurs suffisamment proches de la moyenne de référence pour être considérées équivalentes. L'intervalle, qui repose sur vos connaissances du produit ou du procédé, est défini par une limite d'équivalence inférieure (LEI) et une limite d'équivalence supérieure (LES).
Interprétation
Comparez l'intervalle de confiance aux limites d'équivalence. Si l'intervalle de confiance se trouve entièrement entre les limites d'équivalence, vous pouvez affirmer que la moyenne de la population de test est équivalente à la moyenne de la population de référence. Si une partie de l'intervalle de confiance se trouve en dehors des limites d'équivalence, vous ne pouvez pas affirmer qu'il existe une équivalence.
Différence : moyenne(Générique) - moyenne(Marque)
| Différence | ErT | IC 95% pour équivalence | Intervalle d'équivalence |
|---|---|---|---|
| -0,32104 | 0,060641 | (-0,427349; 0) | (-0,425035; 0,425035) |
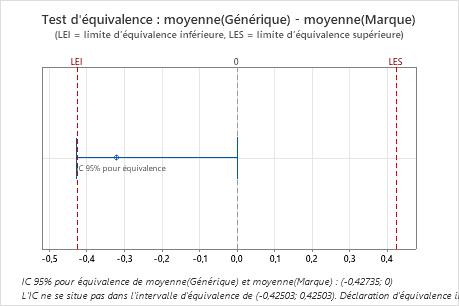
Dans ces résultats, l'intervalle de confiance à 95 % ne se trouve pas complètement dans l'intervalle d'équivalence défini par les limites d'équivalence inférieure (LEI) et supérieure (LES). La borne inférieure de l'intervalle de confiance se prolonge au-delà de la limite d'équivalence inférieure. Vous ne pouvez donc pas en conclure que la moyenne de test équivaut à la moyenne de référence.
Borne inférieure
Minitab affiche une borne de confiance inférieure si vous sélectionnez une hypothèse alternative incluant uniquement une limite inférieure pour la différence (ou le rapport). La borne inférieure indique une valeur à laquelle la différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est susceptible d'être supérieure.
Interprétation
Utilisez la borne de confiance inférieure pour déterminer si la différence (ou le rapport) entre la moyenne de la population de test et la moyenne de la population de référence est supérieure à la borne inférieure. Si la borne de confiance inférieure est supérieure à la limite inférieure, vous pouvez déclarer que la différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est supérieure à la limite inférieure.
Différence : moyenne(Générique) - moyenne(Marque)
| Différence | ErT | Borne inférieure de 95 % | Limite inférieure |
|---|---|---|---|
| -0,32104 | 0,060641 | -0,42735 | -0,42503 |
Dans ces résultats, la borne de confiance à 95 % inférieure pour la différence est −0,42735, valeur inférieure à la limite inférieure de −0,42503. Par conséquent, vous ne pouvez pas déclarer que la différence entre la moyenne de la population du test et la moyenne de la population de référence est supérieure à la limite inférieure.
Borne supérieure
Minitab affiche une borne de confiance supérieure si vous sélectionnez une hypothèse alternative incluant uniquement une limite supérieure pour la différence (ou le rapport). La borne supérieure indique une valeur à laquelle la différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est susceptible d'être inférieure.
Interprétation
Utilisez la borne de confiance supérieure pour déterminer si la différence (ou le rapport) entre la moyenne de la population de test et la moyenne de la population de référence est inférieure à la borne supérieure.Si la borne de confiance supérieure est inférieure à la limite supérieure, vous pouvez déclarer que la différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est inférieure à la limite supérieure.
Différence : moyenne(Générique) - moyenne(Marque)
| Différence | ErT | Borne supérieure de 95 % | Limite supérieure |
|---|---|---|---|
| -0,32104 | 0,060641 | -0,21473 | 0,42503 |
Dans ces résultats, la borne de confiance à 95 % supérieure pour la différence est −0,21473, valeur inférieure à la limite supérieure de 0,42503. Par conséquent, vous pouvez être sûr à 95 % que la différence entre la moyenne de la population du test et la moyenne de la population de référence est inférieure à la limite supérieure.
Limite inférieure
Limite inférieure d'acceptabilité pour la différence (ou le rapport) entre la moyenne du test et la moyenne de référence. La différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est supérieure à la limite inférieure.
Interprétation
Comparez la limite inférieure à la borne de confiance inférieure.Si la borne de confiance inférieure est supérieure à la limite inférieure, vous pouvez déclarer que la différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est supérieure à la limite inférieure.
Différence : moyenne(Générique) - moyenne(Marque)
| Différence | ErT | Borne inférieure de 95 % | Limite inférieure |
|---|---|---|---|
| -0,32104 | 0,060641 | -0,42735 | -0,42503 |
Dans ces résultats, la borne de confiance à 95 % inférieure pour la différence est −0,42735, valeur inférieure à la limite inférieure de −0,42503. Par conséquent, vous ne pouvez pas déclarer que la différence entre la moyenne de la population du test et la moyenne de la population de référence est supérieure à la limite inférieure.
Limite supérieure
Limite supérieure d'acceptabilité pour la différence (ou le rapport) entre la moyenne du test et la moyenne de référence. La différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est inférieure à la limite supérieure.
Interprétation
Comparez la limite supérieure à la borne de confiance supérieure.Si la borne de confiance supérieure est inférieure à la limite supérieure, vous pouvez déclarer que la différence (ou le rapport) entre la moyenne de la population du test et la moyenne de la population de référence est inférieure à la limite supérieure.
Différence : moyenne(Générique) - moyenne(Marque)
| Différence | ErT | Borne supérieure de 95 % | Limite supérieure |
|---|---|---|---|
| -0,32104 | 0,060641 | -0,21473 | 0,42503 |
Dans ces résultats, la borne de confiance à 95 % supérieure pour la différence est −0,21473, valeur inférieure à la limite supérieure de 0,42503. Par conséquent, vous pouvez être sûr à 95 % que la différence entre la moyenne de la population du test et la moyenne de la population de référence est inférieure à la limite supérieure.
