Un ingénieur nutritionniste teste une nouvelle formulation, moins chère, de la nourriture pour chat produite par son entreprise. Il veut s'assurer que la teneur en protéines de la formulation la moins chère est la même que celle de la formulation originale. L'ingénieur mesure la teneur en protéines d'échantillons de 100 grammes des deux formulations pour voir si elles sont équivalentes, à 0,5 grammes près.
L'ingénieur effectue un test d'équivalence à 2 échantillons pour déterminer si la différence moyenne entre les teneurs en protéines des deux formulations ne dépasse pas ± 0,5 g. L'ingénieur ne sait pas si les teneurs en protéines des deux formulations ont la même variance.
- Ouvrez le fichier de données échantillons, ProtéineNourChat.MWX.
- Sélectionnez .
- Dans la liste déroulante, sélectionnez Echantillons dans plusieurs colonnes.
- Dans la zone Echantillon de test, saisissez Prix réduit.
- Dans la zone Echantillon de référence, saisissez Original.
- Dans la fonction Hypothèse sur, sélectionnez Moyenne du test - moyenne de référence.
- Dans la fonction Que souhaitez-vous déterminer ? (Hypothèse alternative), sélectionnez Limite inférieure < moyenne du test - moyenne de référence < limite supérieure.
- Dans la zone Limite inférieure, saisissez –0,5.
- Dans la zone Limite supérieure, saisissez 0,5.
- Cliquez sur OK.
Interprétation des résultats
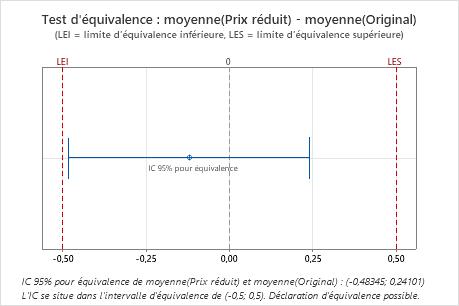
Comme l'intervalle de confiance est entièrement compris dans l'intervalle d'équivalence, l'ingénieur en conclut que les deux recettes de pâtée pour chats contiennent des quantités équivalentes de protéines.
Méthode
Moyenne de référence = moyenne de Original
Les variances n’ont pas été supposées égales pour l’analyse.
Statistiques descriptives
| Variable | N | Moyenne | EcTyp | ErT moyenne |
|---|---|---|---|---|
| Prix réduit | 10 | 33,971 | 0,58064 | 0,18361 |
| Original | 9 | 34,092 | 0,26138 | 0,087127 |
Différence : moyenne(Prix réduit) - moyenne(Original)
| Différence | ErT | IC 95% pour équivalence | Intervalle d'équivalence |
|---|---|---|---|
| -0,12122 | 0,20324 | (-0,483449; 0,241005) | (-0,5; 0,5) |
Test
| Hypothèse nulle : | Différence ≤ -0,5 ou différence ≥ 0,5 |
|---|---|
| Hypothèse alternative : | -0,5 < différence < 0,5 |
| Niveau d'α : | 0,05 |
| Hypothèse nulle | DL | Valeur de T | Valeur de P |
|---|---|---|---|
| Différence ≤ -0,5 | 12 | 1,8637 | 0,044 |
| Différence ≥ 0,5 | 12 | -3,0566 | 0,005 |