Un ingénieur spécialiste de l'emballage souhaite tester une nouvelle méthode de fermeture de sachets à en-cas. La force nécessaire pour ouvrir les sachets ne doit pas s'écarter de plus de 10 % de la valeur cible de 4,2 N (Newtons). L'ingénieur prélève un échantillon aléatoire de 28 sachets fermés à l'aide de la nouvelle méthode et note la force nécessaire pour ouvrir chacun d'entre eux.
L'ingénieur effectue un test d'équivalence à 1 échantillon pour déterminer si la force nécessaire pour ouvrir les sachets dotés de la nouvelle fermeture ne s'écarte pas de plus de 10 % de la valeur cible de 4,2 N.
- Ouvrez le fichier de données échantillons, SachetSnack.MWX.
- Sélectionnez .
- Dans la liste déroulante, sélectionnez Echantillon dans une colonne.
- Dans la zone Echantillons, saisissez Force.
- Dans la zone Cible, saisissez 4,2.
- Dans la fonction Que souhaitez-vous déterminer ? (Hypothèse alternative), sélectionnez Limite inférieure < moyenne du test - cible < limite supérieure.
- Dans la zone Limite inférieure, saisissez –0,1.
- Dans la zone Limite supérieure, saisissez 0,1.
- Sélectionnez Multiplier par la cible.
- Cliquez sur OK.
Interprétation des résultats
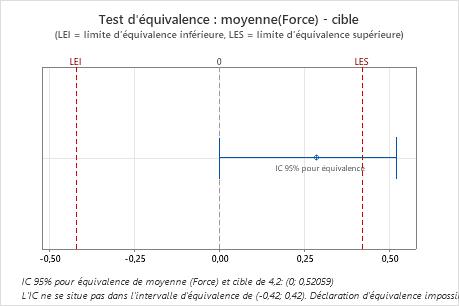
L'intervalle de confiance n'est pas entièrement compris dans l'intervalle d'équivalence. Par conséquent, l'ingénieur ne peut pas déclarer que la force nécessaire pour ouvrir les sachets dotés de la nouvelle fermeture est équivalente à la cible de 4,2 N.
Méthode
Limite d’équivalence inférieure = -0,1 × cible = -0,42
Limite d’équivalence supérieure = 0,1 × cible = 0,42
Statistiques descriptives
| Variable | N | Moyenne | EcTyp | ErT moyenne |
|---|---|---|---|---|
| Force | 28 | 4,4850 | 0,73188 | 0,13831 |
Différence : moyenne(Force) - cible
| Différence | ErT | IC 95% pour équivalence | Intervalle d'équivalence |
|---|---|---|---|
| 0,28500 | 0,13831 | (0; 0,520586) | (-0,42; 0,42) |
Test
| Hypothèse nulle : | Différence ≤ -0,42 ou différence ≥ 0,42 |
|---|---|
| Hypothèse alternative : | -0,42 < différence < 0,42 |
| Niveau d'α : | 0,05 |
| Hypothèse nulle | DL | Valeur de T | Valeur de P |
|---|---|---|---|
| Différence ≤ -0,42 | 27 | 5,0972 | 0,000 |
| Différence ≥ 0,42 | 27 | -0,97605 | 0,169 |