La valeur de Z est une statistique de test pour les tests Z qui mesure la différence entre une statistique observée et son paramètre de population hypothétisé, en unités d'écart type. Par exemple, une sélection de moules industriels présente une profondeur moyenne de 10 cm et un écart type de 1 cm. Un moule d'une profondeur de 12 cm possède une valeur de Z égale à 2, car sa profondeur est supérieure de deux écarts types à la moyenne. La ligne verticale ci-après représente cette observation et son emplacement par rapport au reste de la population :
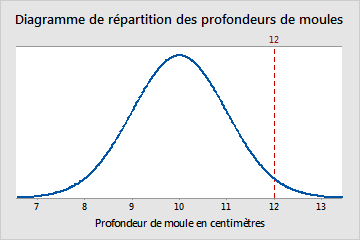
La conversion d'une observation en une valeur de Z est appelée normalisation. Pour normaliser une observation dans une population, soustrayez la moyenne de population de l'observation qui vous intéresse, puis divisez le résultat par l'écart type de la population. Ces calculs génèrent la valeur de Z associée à l'observation qui vous intéresse.
Vous pouvez utiliser la valeur de Z afin de déterminer si l'hypothèse nulle doit être rejetée. Pour ce faire, comparez la valeur de Z à votre valeur critique, que vous trouverez dans un tableau normal standard dans la plupart des ouvrages de statistiques. La valeur critique est Z1-α/2 pour un test bilatéral et Z1-α pour un test unilatéral. Si la valeur absolue de Z est supérieure à la valeur critique, vous rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle.
Par exemple, vous souhaitez savoir si un second groupe de moules présente également une profondeur moyenne de 10 cm. Vous mesurez la profondeur de chaque moule du second groupe, puis vous calculez la profondeur moyenne du groupe. Un test Z à 1 échantillon calcule une valeur de Z de −1,03. Vous choisissez une valeur α de 0,05, ce qui donne pour résultat une valeur critique de 1,96. Comme la valeur absolue de Z est inférieure à 1,96, vous ne rejetez pas l'hypothèse nulle et ne pouvez pas conclure que la profondeur moyenne du moule est différente de 10 cm.
