Les degrés de libertés (DL) représentent la quantité d'informations fournies par les données que vous pouvez "consommer" pour estimer les valeurs des paramètres de population inconnus et calculer la variabilité de ces estimations. Cette valeur est déterminée par le nombre d'observations dans votre échantillon et le nombre de paramètres dans votre modèle.
L'accroissement de l'effectif de l'échantillon permet d'obtenir davantage d'informations sur la population, ce qui augmente les degrés de liberté présents dans les données. L'ajout de paramètres au modèle (en augmentant le nombre de termes dans une équation de régression, par exemple) "consomme" des informations dans les données et diminue les degrés de liberté disponibles pour évaluer la variabilité des estimations des paramètres.
Les degrés de liberté permettent également de caractériser une loi de distribution particulière. Par exemple, de nombreuses familles de lois de distribution (comme les lois t, F et du Khi deux) utilisent des degrés de liberté pour déterminer spécifiquement quelle est la loi t, F ou du Khi deux adaptée suivant l'effectif de l'échantillon et le nombre de paramètres dans le modèle. Par exemple, la figure ci-dessous compare différentes lois du Khi deux en fonction de leur nombre de degrés de liberté.
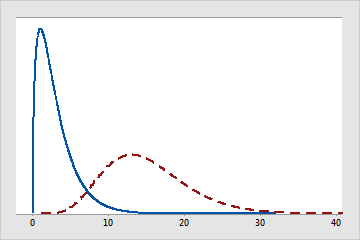
Lois du Khi deux avec différents degrés de liberté
La loi de distribution à ligne continue possède 3 degrés de liberté. La loi de distribution à ligne en pointillés possède 15 degrés de liberté.
Exemples
Par exemple, le test t à 1 échantillon estime un seul paramètre : la moyenne. L'effectif d'échantillon n constitue n éléments d'information pour l'estimation de la moyenne de la population et de sa variabilité. Un degré de liberté est consommé pour estimer la moyenne, tandis que les autres n-1 degrés de liberté permettent d'évaluer la variabilité. Par conséquent, un test t à 1 échantillon utilise une loi t avec n-1 degrés de liberté.
A l'inverse, une régression linéaire multiple doit estimer un paramètre pour chaque terme que vous choisissez d'inclure dans le modèle et chacun consomme un degré de liberté. Par conséquent, l'inclusion d'un nombre excessif de termes dans un modèle de régression linéaire multiple réduit le nombre de degrés de liberté disponibles pour estimer la variabilité des paramètres et peut rendre le modèle moins fiable.
