Lorsque vous cherchez à déterminer des informations sur une caractéristique de population en particulier (par exemple, la moyenne), vous prenez généralement un échantillon aléatoire de cette population car il est impossible de mesurer une population entière. A l'aide de cet échantillon, vous calculez la caractéristique d'échantillon correspondante, qui est utilisée pour obtenir des informations récapitulatives sur la caractéristique de population inconnue. La caractéristique de population qui vous intéresse est appelée paramètre et la caractéristique d'échantillon correspondante est nommée statistique issue de l'échantillon ou estimation du paramètre. Etant donné que la statistique est un récapitulatif des informations sur un paramètre, obtenues à partir de l'échantillon, la valeur d'une statistique dépend de l'échantillon spécifique qui a été prélevé de la population. Sa valeur change aléatoirement d'un échantillon à l'autre, et une statistique est donc une quantité aléatoire (variable). La loi de probabilité de cette variable aléatoire est appelée loi d'échantillonnage. La loi d'échantillonnage d'une statistique (d'échantillon) est importante, car elle permet de tirer des conclusions sur le paramètre de population correspondant à partir d'un échantillon aléatoire.
Par exemple, lorsqu'un échantillon aléatoire est prélevé d'une population suivant une loi normale, la moyenne de l'échantillon est une statistique. La valeur de cette moyenne, obtenue à partir de l'échantillon utilisé, est une estimation de la moyenne de la population. Cette valeur estimée change de manière aléatoire si un autre échantillon est prélevé dans la même population normale. La loi de probabilité qui décrit ces changements est la loi d'échantillonnage de la moyenne de l'échantillon. La loi d'échantillonnage d'une statistique indique toutes les valeurs possibles d'une statistique et la fréquence d'une certaine plage de valeurs de la statistique. Dans le cas où la population parent est normale, la loi d'échantillonnage de la moyenne de l'échantillon l'est également.
Les sections suivantes fournissent plus d'informations sur les paramètres, estimations de paramètres et lois d'échantillonnage.
A propos des paramètres
Les paramètres sont des mesures descriptives de la totalité d'une population, qui peuvent être utilisées comme valeurs d'entrée d'une fonction de densité de probabilité (PDF) pour générer des courbes de distribution. Les paramètres sont généralement désignés par des lettres grecques afin qu'ils soient différenciés des statistiques issues de l'échantillon. Par exemple, la moyenne de la population est représentée par la lettre grecque mu (µ) et l'écart type de la population par la lettre grecque sigma (σ). Les paramètres sont des constantes fixes, autrement dit, ils ne fluctuent pas comme les variables. Toutefois, leurs valeurs sont généralement inconnues, car il est impossible de mesurer une population entière.
| Loi de distribution | Paramètre 1 | Paramètre 2 | Paramètre 3 |
|---|---|---|---|
| Khi deux | Degrés de liberté | ||
| Normale | Moyenne | Ecart type | |
| Gamma 3 paramètres | Forme | Echelle | Seuil |
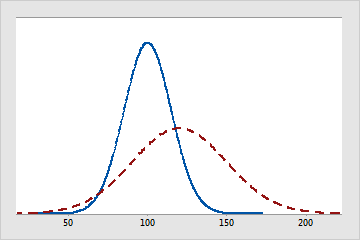
La ligne en trait plein représente une loi de distribution normale avec une moyenne de 100 et un écart type de 15. La ligne en pointillés représente également une loi normale, mais sa moyenne est de 120 et son écart type de 30.
A propos des estimations des paramètres (statistiques issues des échantillons)
Les paramètres sont des mesures descriptives de la totalité d'une population. Toutefois, leurs valeurs sont généralement inconnues, car il est impossible de mesurer une population entière. Pour cette raison, vous pouvez prélever un échantillon aléatoire dans la population afin d'obtenir des estimations des paramètres. L'un des objectifs des analyses statistiques consiste à obtenir des estimations des paramètres de la population ainsi que l'importance d'erreur associée à ces estimations. Ces estimations sont également appelées "statistiques issues des échantillons".
- Les estimations ponctuelles constituent la valeur unique la plus probable d'un paramètre. Par exemple, l'estimation ponctuelle de la moyenne de la population (le paramètre) est la moyenne de l'échantillon (l'estimation du paramètre).
- Les intervalles de confiance correspondent à une plage de valeurs susceptible de contenir le paramètre de la population.
Pour vous donner un exemple des estimations des paramètres, supposons que vous travailliez pour un fabricant de bougies d'allumage qui étudie un problème relatif à l'écartement des électrodes. L'évaluation de chaque bougie d'allumage serait trop onéreuse. A la place, vous pouvez échantillonner de façon aléatoire 100 bougies d'allumage et en mesurer l'écartement en millimètres. La moyenne de l'échantillon est de 9,2. Il s'agit de l'estimation ponctuelle pour la moyenne de la population (µ). En outre, vous créez un intervalle de confiance à 95 % pour µ, en l'occurrence (8,8, 9,6). Cela signifie que vous pouvez être sûr à 95 % que la véritable valeur de l'écartement moyen pour toutes les bougies d'allumage est comprise entre 8,8 et 9,6.
A propos des distributions d'échantillonnage
| Citrouille | 1 | 2 | 3 | 4 | 5 | 6 |
| Poids | 19 | 14 | 15 | 12 | 16 | 17 |
Même si la population entière est connue, pour les besoins de l'exemple, nous prenons tous les échantillons aléatoires possibles de la population qui contiennent 3 citrouilles (20 échantillons aléatoires). Ensuite, nous calculons la moyenne de chaque échantillon. La loi d'échantillonnage de la moyenne issue des échantillons est décrite par toutes les moyennes d'échantillon pour tout échantillon aléatoire possible de 3 citrouilles, comme indiqué dans le tableau ci-dessous.
| Echantillon | Poids | Poids moyen | Probabilité |
|---|---|---|---|
| 2, 3, 4 | 14, 15, 12 | 13,7 | 1/20 |
| 2, 4, 5 | 14, 12, 16 | 14 | 1/20 |
| 2, 4, 6 | 14, 12, 17 | 14,3 | 2/20 |
| 3, 4, 5 | 15, 12, 16 | ||
| 3, 4, 6 | 15, 12, 17 | 14,7 | 1/20 |
| 1, 2, 4 | 19, 14, 12 | 15 | 3/20 |
| 2, 3, 5 | 14, 15, 16 | ||
| 4, 5, 6 | 12, 16, 17 | ||
| 2, 3, 6 | 14, 15, 17 | 15,3 | 2/20 |
| 1, 3, 4 | 19, 15, 12 | ||
| 1, 4, 5 | 19, 12, 16 | 15,7 | 2/20 |
| 2, 5, 6 | 14, 16, 17 | ||
| 1, 2, 3 | 19, 14, 15 | 16 | 3/20 |
| 3, 5, 6 | 15, 16, 17 | ||
| 1, 4, 6 | 19, 12, 17 | ||
| 1, 2, 5 | 19, 14, 16 | 16,3 | 1/20 |
| 1, 2, 6 | 19, 14, 17 | 16,7 | 2/20 |
| 1, 3, 5 | 19, 15, 16 | ||
| 1, 3, 6 | 19, 15, 17 | 17 | 1/20 |
| 1, 5, 6 | 19, 16, 17 | 17,3 | 1/20 |
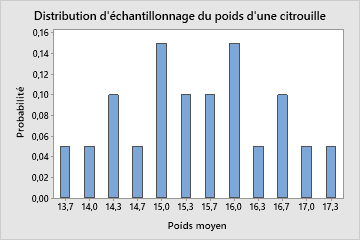
En pratique, présenter sous forme de tableau la distribution de la loi d'échantillonnage comme dans l'exemple ci-dessus est irréalisable. Même dans le meilleur des cas, si vous connaissez la population parent des échantillons, vous ne pourrez sans doute pas déterminer la loi d'échantillonnage exacte des statistiques issues des échantillons qui vous intéressent. Dans certains cas, cependant, vous pourrez déterminer approximativement la loi d'échantillonnage de ces statistiques. Par exemple, si vous prenez des échantillons dans une population normale, la moyenne issue des échantillons suit exactement la loi normale.
En revanche, si vous prélevez des échantillons dans une population non normale, vous ne pourrez peut-être pas déterminer exactement la loi de distribution de la moyenne d'échantillon. Cela dit, en vertu du théorème central limite, la moyenne d'échantillon suit une loi à peu près normale, à condition que vos échantillons soient suffisamment grands. Ainsi, si la population est inconnue et que vos échantillons sont suffisamment grands, vous pourriez par exemple être en mesure d'affirmer avec 85 % de certitude que la moyenne de l'échantillon se situe à moins d'un certain nombre d'écarts types de la moyenne de la population.
