L'asymétrie et l'aplatissement de vos données vous permettent de vous en faire une première idée.
Sur ce thème
Asymétrie
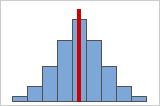
Figure A
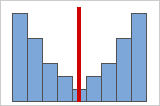
Figure B
Distributions symétriques ou non asymétriques
Plus des données sont symétriques, plus leur valeur d'asymétrie approche de zéro. La figure A montre des données distribuées normalement qui, par définition, présentent une asymétrie relativement faible. Si vous traciez une ligne verticale au milieu de cet histogramme de données normales, vous pourriez facilement constater que les deux côtés se reflètent l'un l'autre. Toutefois, l'absence d'asymétrie n'est pas en soi synonyme de normalité. La figure B représente une loi de distribution dont les deux côtés se reflètent également, mais les données sont loin d'être distribuées normalement.
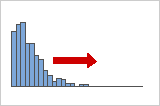
Distributions positives ou asymétriques à droite
Les données présentant une asymétrie positive ou asymétriques à droite doivent leur appellation au fait que la "queue" de la loi de distribution pointe vers la droite et que leur valeur d'asymétrie est supérieure à 0 (ou est positive). Les données salariales présentent souvent une asymétrie de ce type : au sein d'une entreprise, de nombreux employés gagnent relativement peu et, à mesure que les salaires augmentent, le nombre d'employés concernés diminue.
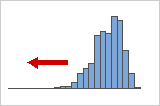
Distributions négatives ou asymétriques à gauche
Les données asymétriques à gauche ou présentant une asymétrie négative doivent leur nom au fait que la "queue" de leur loi de distribution pointe vers la gauche et qu'elles génèrent une valeur d'asymétrie négative. Les données sur les taux de défaillance sont souvent asymétriques à gauche. Prenez par exemple le cas d'ampoules électriques : très peu vont griller immédiatement, la très grande majorité ayant une durée de vie assez longue.
Aplatissement
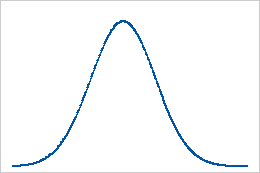
Référence : valeur d'aplatissement de 0
Les données qui suivent parfaitement une loi normale ont une valeur d'aplatissement de 0. Des données distribuées normalement établissent la référence de l'aplatissement. Un aplatissement déviant significativement de la valeur 0 peut indiquer que les données ne sont pas distribuées normalement.
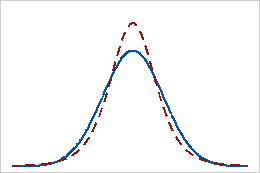
Aplatissement positif
Les données ayant une valeur d'aplatissement positive présentent des queues plus lourdes qu'avec la loi normale. Par exemple, les données qui suivent une loi t ont une valeur d'aplatissement positive. La ligne pleine représente la loi normale et la ligne en pointillés représente une loi de distribution possédant une valeur d'aplatissement positive.
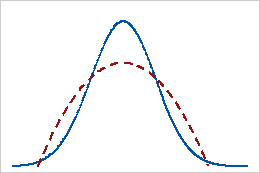
Aplatissement négatif
Les données ayant une valeur d'aplatissement négative présentent des queues plus légères qu'avec la loi normale. Par exemple, les données qui suivent une loi bêta avec un premier et un deuxième paramètres de forme égaux à 2 ont une valeur d'aplatissement négative. La ligne pleine représente la loi normale et la ligne en pointillés représente une loi de distribution possédant une valeur d'aplatissement négative.
