Le théorème central limite est un théorème fondamental du domaine de la probabilité et des statistiques. Il décrit la loi de distribution de la moyenne d'un échantillon aléatoire provenant d'une population avec une variance limitée. Lorsque l'effectif de l'échantillon est suffisament large, la loi de distribution des moyennes est à peu près normale. Le théorème s'applique quelle que soit la forme de la loi de distribution de la population. De nombreuses procédures de statistiques communes nécessitent que les données soient à peu près normales. Le théorème central limite vous permet d'appliquer ces procédure efficaces aux populations fortement anormales. La taille que doit présenter l'effectif de l'échantillon dépend de la forme de la loi de distribution initiale. Si la distribution de la population est symétrique, l'effectif d'un échantillon de 5 pourra générer une bonne approximation. Si la distribution de la population est fortement asymétrique, un effectif d'échantillon plus important est nécessaire. Par exemple, la loi de distribution de la moyenne peut être à peu près normale si l'effectif de l'échantillon est supérieur à 50. Les graphiques suivants présentent des exemples de l'incidence de la loi de distribution sur l'effectif d'échantillon nécessaire.
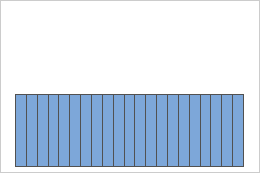
Loi uniforme
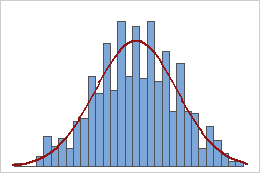
Moyennes des échantillons
Echantillons issus d'une population uniforme
Une population qui suit une loi uniforme est symétrique mais fortement non normal comme le démontre de premier histogramme. Toutefois, la distribution des moyennes de l'échantillon à partir de 1000 échantillons d'effectif 5 tirés de cette population est à peu près normale en raison du théorème central limite, comme le montre le second histogramme. Cet histogramme des moyennes de l'échantillon comprend une courbe normale superposée qui illustre cette normalité.
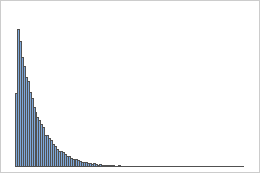
Loi exponentielle
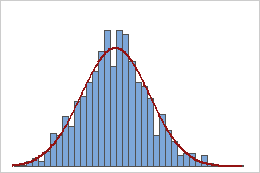
Moyennes des échantillons
Echantillons issus d'une population exponentielle
Une population qui suit une loi exponentielle est asymétrique et non normale, comme l'illustre le premier histogramme. Toutefois, la distribution des moyennes de l'échantillon à partir de 1000 échantillons d'effectif 50 tirés de cette population est à peu près normale en raison du théorème central limite, comme le montre le second histogramme. Cet histogramme des moyennes de l'échantillon comprend une courbe normale superposée qui illustre cette normalité.
