Qu'est‑ce que la corrélation ?
- Coefficient de corrélation produit-moment de Pearson
-
La corrélation de Pearson évalue la relation linéaire entre deux variables continues. Une relation est dite linéaire lorsqu'une modification de l'une des variables est associée à une modification proportionnelle de l'autre variable.
Par exemple, vous pouvez utiliser une corrélation de Pearson afin d'évaluer si les augmentations de température sur votre site de production sont associées à la diminution de l'épaisseur de votre enrobage de chocolat.
- Coefficient de corrélation rang-ordre de Spearman
-
La corrélation de Spearman évalue la relation monotone entre deux variables continues ou ordinales. Dans une relation monotone, les variables ont tendance à changer ensemble, mais pas forcément à une vitesse constante. Le coefficient de corrélation de Spearman est fondé sur les valeurs classées pour chaque variable plutôt que sur les données brutes.
La corrélation de Spearman est souvent utilisée dans le but d'évaluer les relations comprenant des variables ordinales. Par exemple, vous pouvez utiliser une corrélation de Spearman afin d'évaluer si l'ordre dans lequel des employés effectuent un exercice d'un test est lié au nombre de mois d'ancienneté.
Il est toujours judicieux d'examiner la relation entre les variables à l'aide d'un nuage de points. Les coefficients de corrélation ne mesurent que des relations linéaires (Pearson) ou monotones (Spearman). D'autres relations sont possibles.
Comparaison des coefficients de Pearson et de Spearman

Pearson = +1, Spearman = +1
Si dans la relation, une variable augmente lorsque l'autre augmente, mais que cette augmentation n'est pas constante, le coefficient de corrélation de Pearson est positif mais inférieur à +1. Dans ce cas, le coefficient de Spearman est lui toujours égal à +1.

Pearson = +0,851, Spearman = +1

Pearson = −0,093, Spearman = −0,093

Pearson = −1, Spearman = −1

Pearson = −0,799, Spearman = −1
Les valeurs de corrélation -1 ou 1 impliquent une relation linéaire exacte, à l'image de celle entre le rayon et la circonférence d'un cercle. Toutefois, le véritable intérêt des valeurs de corrélation est de permettre la quantification de relations non parfaites. L'existence d'une corrélation entre deux variables est souvent une information importante pour une analyse de régression qui essaie d'affiner la description de ce type de relation.
Autres relations non linéaires
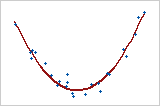
Coefficient de 0
Ce graphique révèle une très forte relation. Les coefficients de Pearson et de Spearman sont tous deux proches de 0.
