Un intervalle de confiance est une plage de valeurs issue des statistiques d'échantillons et ayant de grandes chances de contenir la valeur d'un paramètre de population inconnu. En raison de leur nature aléatoire, il est peu probable que deux échantillons d'une population donnée génèrent des intervalles de confiance identiques. Par contre, si vous répétiez l'échantillonnage de nombreuses fois, un certain pourcentage des intervalles de confiance obtenus contiendrait le paramètre de population inconnu.
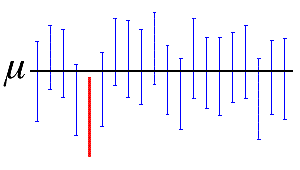
Sur ce graphique, la ligne noire horizontale représente la valeur fixe de la moyenne de population inconnue, µ. Les intervalles de confiance bleus verticaux qui chevauchent la ligne horizontale comprennent la valeur de la moyenne de population. Ce qui n'est pas le cas de l'intervalle de confiance rouge situé complètement en dessous la ligne horizontale. Un intervalle de confiance à 95 % indique que 19 échantillons sur 20 (95 %) d'une même population génèrent des intervalles de confiance qui contiennent le paramètre de population.
Utilisez l'intervalle de confiance pour évaluer l'estimation du paramètre de population. Par exemple, un fabricant souhaite savoir si la longueur moyenne des crayons qu'il produit diffère de la longueur cible. Il prélève un échantillon aléatoire de crayons et détermine que la longueur moyenne pour cet échantillon est de 52 millimètres et que l'intervalle de confiance à 95 % est (50,54). Par conséquent, il peut être sûr à 95 % que la longueur moyenne de tous les crayons est comprise entre 50 et 54 millimètres.
- Estimation ponctuelle
- Cette valeur unique estime un paramètre de population à l'aide de vos données échantillons.
- Marge d'erreur
-
Lorsque vous utilisez des statistiques pour estimer une valeur, il est important de se rappeler que, même si votre étude est très bien conçue, votre estimation est sujette à une erreur d'échantillonnage aléatoire. La marge d'erreur quantifie cette erreur et indique la précision de votre estimation.
Vous connaissez probablement la notion de marge d'erreur, qui est notamment utilisée pour les résultats de sondages. Par exemple, un sondage politique peut indiquer que la cote de popularité d'un candidat est de 55 % avec une marge d'erreur de 5 %. Cela signifie que la cote de popularité réelle se situe dans une fourchette comprise entre 5 points au-dessus et 5 points au-dessous de la valeur estimée, soit entre 50 % et 60 %.
Pour un intervalle de confiance bilatéral, la marge d'erreur correspond à la distance entre la statistique estimée et chaque valeur constituant l'intervalle de confiance. Lorsqu'un intervalle de confiance est symétrique, la marge d'erreur est égale à la moitié de la largeur de l'intervalle de confiance. Par exemple, la longueur estimée moyenne d'un arbre à cames est de 600 mm et l'intervalle de confiance s'étend de 599 à 601. La marge d'erreur est de 1.
Plus la marge d'erreur est élevée, plus l'intervalle est large et moins vous pouvez être certain de la valeur de l'estimation ponctuelle.
