Lorsque vous évaluez la relation entre deux variables, il est important de déterminer la relation entre les variables. Les relations linéaires sont les plus fréquentes, mais les variables peuvent aussi avoir une relation non linéaire ou monotone, comme illustré ci-dessous. Il est également possible qu'il n'existe aucune relation entre les variables. Vous devriez commencer par créer un nuage de points des variables pour évaluer leur relation.
Une relation linéaire est une tendance dans les données modélisable par une ligne droite. Par exemple, supposons qu'une compagnie aérienne souhaite estimer l'impact du prix du carburant sur le coût des vols. Elle constate que pour chaque augmentation d'un dollar du prix d'un gallon de carburéacteur, le coût de son vol Los Angeles-New York augmente d'environ 3500 dollars. Cette tendance décrit une relation linéaire entre le coût du carburéacteur et le coût du vol.
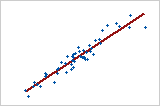
Diagramme 1 : forte relation linéaire positive
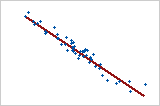
Diagramme 2 : forte relation linéaire négative
Lorsque les deux variables augmentent ou diminuent simultanément et à une vitesse constante, une relation linéaire positive existe. Dans le diagramme 1, les points suivent la ligne de près, suggérant que la relation entre les variables est forte. Le coefficient de corrélation de Pearson pour cette relation est +0,921.
Lorsqu'une variable augmente alors que l'autre diminue, il existe une relation linéaire négative. Dans le diagramme 2, les points suivent la ligne de près, suggérant que la relation entre les variables est forte. Le coefficient de corrélation de Pearson pour cette relation est -0,968.
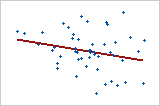
Diagramme 3 : faible relation linéaire
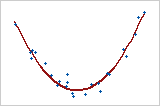
Diagramme 4 : relation non linéaire
Dans le diagramme 3, les points de données présentent une distribution aléatoire. Ils ne sont pas proches de la ligne, ce qui signifie que la relation est très faible, si relation il y a. Le coefficient de corrélation de Pearson pour cette relation est -0,253.
Si une relation entre deux variables n'est pas linéaire, le taux d'augmentation ou de diminution peut changer lorsqu'une variable évolue, créant un "schéma en courbe" dans les données. Cette tendance en courbe pourrait éventuellement être mieux modélisée par une fonction non linéaire, telle qu'une fonction quadratique ou cubique, ou être transformée afin qu'elle soit linéaire. Le diagramme 4 fait apparaître une forte relation entre deux variables. Cependant, comme cette relation n'est pas linéaire, le coefficient de corrélation de Pearson n'est que de +0,244. Cette relation illustre la raison pour laquelle il est important de représenter les données graphiquement, afin d'analyser tous les types de relations qui peuvent exister.
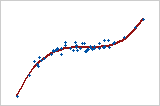
Diagramme 5 : relation monotone
Dans une relation monotone, les variables ont tendance à se déplacer dans la même direction relative, mais pas forcément à une vitesse constante. Dans une relation linéaire, les variables se déplacent dans la même direction, à une vitesse constante. Le diagramme 5 montre que les variables augmentent simultanément, mais pas à la même vitesse. Cette relation est monotone, mais pas linéaire. Le coefficient de corrélation de Pearson pour ces données est 0,843, mais celui de la corrélation de Spearman est plus élevé, 0,948.
Les relations linéaires sont également monotones. Par exemple, la relation indiquée sur le diagramme 1 est à la fois monotone et linéaire.
