Sur ce thème
Moyenne
La moyenne est une mesure courante du centre d'un ensemble de valeurs numériques. Il s'agit de la somme de toutes les observations divisée par le nombre d'observations (présentes).
Formule
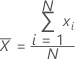
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
| N | nombre d'observations présentes |
Erreur type de la moyenne (ErT moyenne)
L'erreur type de la moyenne est la division de l'écart type par la racine carrée de l'effectif d'échantillon.
Formule

Notation
| Terme | Description |
|---|---|
| s | écart type de l'échantillon |
| N | nombre d'observations présentes |
Ecart type (EcTyp)
L'écart type de l'échantillon fournit une mesure de l'étendue de vos données. Il est égal à la racine carrée de la variance de l'échantillon.
Formule
 , l'écart type de l'échantillon est :
, l'écart type de l'échantillon est :
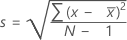
Notation
| Terme | Description |
|---|---|
| x i | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
Variance
La variance mesure le degré de dispersion des données autour de leur moyenne. Elle est égale à l'écart type au carré.
Formule
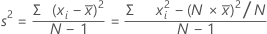
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
Coefficient de variation (CoefVar)
Le coefficient de variation est une mesure de variabilité calculée sous forme de pourcentage.
Formule

Minitab le calcule comme suit :

Notation
| Terme | Description |
|---|---|
| s | écart type de l'échantillon |
 | moyenne des observations |
1er quartile (Q1)
25 % de vos observations d'échantillon sont inférieures ou égales à la valeur du 1er quartile. Donc, le 1er quartile est également le 25e percentile.
Formule

Notation
| Terme | Description |
|---|---|
| y | valeur d'entier tronqué de w |
| w | 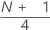 |
| z | composant de fraction de w tronqué |
| xj | je observation de la liste de données d'échantillon, classées de la plus petite à la plus grande |
Remarque
Lorsque x est un entier, y = w, z = 0 et Q1 = xy.
Médiane
La médiane de l'échantillon se trouve au milieu des données : au moins la moitié des observations lui est inférieure ou égale, et au moins la moitié lui est supérieure ou égale.
Supposez qu'une colonne contient N valeurs. Pour calculer la médiane, vous devez d'abord classer vos valeurs de données de la plus petite à la plus grande. Si N est impair, la médiane de l'échantillon est la valeur centrale. Si N est pair, la médiane de l'échantillon est la moyenne des deux valeurs centrales.
Par exemple, lorsque N = 5 et que vous avez les données x1, x2, x3, x4 et x5, la médiane est = x3.
Lorsque N = 6 et que vous avez classé les données x1, x2, x3, x4, x5 et x6 :
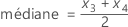
où x3 et x4 sont les troisième et quatrième observations.
3e quartile (Q3)
75 % de vos observations d'échantillon sont inférieures ou égales à la valeur du troisième quartile. Donc, le troisième quartile est également le 75e percentile.
Formule

Notation
| Terme | Description |
|---|---|
| y | valeur tronquée de w |
| w |
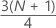 |
| z | composant de fraction de w tronqué |
| xj | je observation de la liste de données d'échantillon, classées de la plus petite à la plus grande |
Remarque
Lorsque w est un entier, y = w, z = 0 et Q3 = xy.
Etendue interquartile (EIQ)
L'étendue interquartile est égale au troisième quartile mois le 1er quartile.
Moyenne tronquée (MoyTronquée)
Minitab calcule la moyenne tronquée en enlevant les 5 % les plus petits et les 5 % les plus grands (arrondis à l'entier le plus proche), puis en calculant la moyenne des valeurs restantes.
Somme
Formule

Notation
| Terme | Description |
|---|---|
| xi | ie observation |
Minimum
Plus petite valeur de votre ensemble de données.
Maximum
Plus grande valeur de votre ensemble de données.
Etendue
L'étendue est la différence entre la plus grande valeur des données et la plus petite.
R = Maximum – Minimum
Somme des carrés
Minitab élève au carré chaque valeur dans la colonne, puis calcule la somme de ces carrés.
Formule
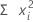
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
Asymétrie
Il s'agit d'une mesure de l'asymétrie. Une valeur négative indique une asymétrie vers la gauche, tandis qu'une valeur positive indique une asymétrie vers la droite. Une valeur nulle n'indique pas forcément une symétrie.
Formule
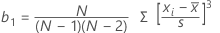
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
| s | écart type de l'échantillon |
Aplatissement
L'aplatissement est une mesure de la différence d'une loi distribution par rapport à une loi normale. Une valeur positive indique généralement que la loi a un pic plus aigu que la distribution normale. Une valeur négative indique que la loi a un pic moins aigu que la distribution normale.
Formule

Notation
| Terme | Description |
|---|---|
| xi | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
| s | écart type de l'échantillon |
MSSD (Moyenne des différences successives carrées)
Minitab calcule une demi MSSD (moyenne des différences successives carrées) d'un ensemble de nombres. Les différences successives sont mises au carré puis additionnées. Ensuite, Minitab divise le résultat par 2 et calcule la moyenne.
Formule
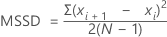
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
 | moyenne des observations |
Nombre de valeurs présentes (N)
Nombre de valeurs présentes dans votre échantillon.
Nombre de valeurs manquantes (N*)
Nombre de valeurs manquantes dans votre échantillon. Le nombre de valeurs manquantes correspond au nombre de cellules contenant le symbole de valeur manquante *.
Nombre de valeurs total (dénombrement total)
Nombre total d'observations dans la colonne.
Pourcentage
Minitab calcule le pourcentage de chaque groupe par rapport au total.
Formule

Notation
| Terme | Description |
|---|---|
| ni | nombre d'observations dans le ie groupe |
| N | nombre d'observations présentes |
Pourcentage cumulé (%Cum)
Minitab calcule le pourcentage cumulé représenté par chaque groupe.
Formule
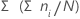
Notation
| Terme | Description |
|---|---|
| ni | nombre d'observations dans le ie groupe |
| N | nombre d'observations présentes |
