Sur ce thème
Etape 1 : Déterminer un intervalle de confiance pour la différence de moyenne de la population
Considérez d'abord la différence moyenne, puis examinez l'intervalle de confiance. La différence moyenne représente la moyenne des différences entre les observations appariées de votre échantillon.
La différence moyenne est une estimation de la différence moyenne de la population. La différence moyenne étant calculée à partir des données d'échantillon et non de l'ensemble de la population, il est peu probable que la différence moyenne de l'échantillon soit égale à celle de la population. Pour mieux estimer la différence moyenne de la population, utilisez l'intervalle de confiance de la différence.
L'intervalle de confiance fournit une étendue de valeurs probables pour la différence moyenne de la population entre les observations appariées. Par exemple, un niveau de confiance de 95 % indique que, sur 100 échantillons pris de façon aléatoire parmi la population, environ 95 de ces échantillons devraient produire des intervalles contenant la différence moyenne de population. L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon. Pour plus d'informations, reportez-vous à la rubrique Obtenir un intervalle de confiance plus précis.
Estimation de la différence pour données appariées
| Moyenne | EcTyp | ErT moyenne | IC à 95% pour μ_différence |
|---|---|---|---|
| 2,200 | 3,254 | 0,728 | (0,677; 3,723) |
Résultats principaux : différence moyenne, intervalle de confiance à 95 % pour la différence de moyenne
Dans ces résultats, l'estimation de la différence moyenne de la population en matière de fréquence cardiaque est de 2,2. Vous pouvez être sûr à 95 % que la différence moyenne de la population est comprise entre 0,677 et 3,723.
Etape 2 : Déterminer si les résultats du test sont statistiquement significatifs
- Valeur de p ≤ α : la différence entre les moyennes est statistiquement significative (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle. Vous pouvez conclure que la différence entre les moyennes de population n'est pas égale à la différence hypothétisée. Si vous n'avez pas indiqué de différence hypothétisée, Minitab teste l'absence de différence entre les moyennes (Différence hypothétisée = 0) Utilisez vos connaissances afin de déterminer si la différence est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Signification statistique et pratique.
- Valeur de p > α : la différence entre les moyennes n'est pas statistiquement significative (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que la différence des moyennes des observations appariées est statistiquement significative. Vous devez vous assurer que votre test est assez puissant pour détecter une différence qui est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Puissance et effectif de l'échantillon pour un test t pour données appariées.
Test
| Hypothèse nulle | H₀ : μ_différence = 0 |
|---|---|
| Hypothèse alternative | H₁ : μ_différence ≠ 0 |
| Valeur de T | Valeur de P |
|---|---|
| 3,02 | 0,007 |
Résultat principal : valeur de p
Dans ces résultats, l'hypothèse nulle indique que la différence moyenne des rythmes cardiaques au repos pour les patients avant et après un programme de course est de 0. La valeur de p étant 0,007, ce qui est inférieur au seuil de signification de 0,05, il faut rejeter l'hypothèse nulle et conclure qu'il existe une différence entre les rythmes cardiaques des patients avant et après le programme de course.
Etape 3 : rechercher les problèmes dans les données
Certains problèmes avec les données, comme la présence d'une asymétrie ou de valeurs aberrantes, risquent de nuire à vos résultats. Utilisez les graphiques pour rechercher toute asymétrie et pour détecter d'éventuelles valeurs aberrantes.
Examinez la dispersion des données pour déterminer si elles semblent asymétriques.
Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
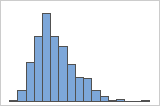
Asymétrie à droite
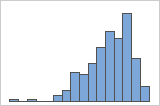
Asymétrie vers la gauche
L'histogramme avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. L'histogramme avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
Les données qui sont très asymétriques peuvent avoir une incidence sur la validité de la valeur de p si votre échantillon est petit (moins de 20 valeurs). Si vos données sont très asymétriques et que vous avez un petit échantillon, pensez éventuellement à augmenter l'effectif d'échantillon.
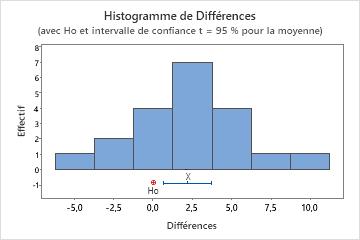
Dans cet histogramme, les données ne semblent pas sérieusement asymétriques.
Identification des valeurs aberrantes
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
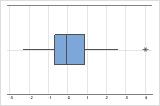
Sur une boîte à moustaches, les astérisques (*) indiquent les valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
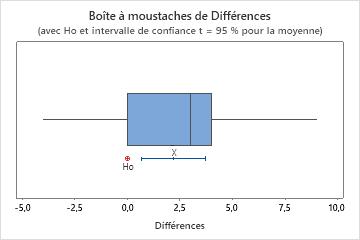
Il n'y a aucune valeur aberrante dans cette boîte à moustaches.
