Définissez le test, le seuil de signification et sélectionnez l'hypothèse alternative.
Sur ce thème
Test des valeurs aberrantes
Tous les tests de valeurs aberrantes de Minitab sont conçus pour détecter une seule valeur aberrante dans un échantillon. Généralement, le test de Grubb fonctionne bien. Cependant, si un échantillon contient plus d'une valeur aberrante potentielle, le test de Grubb et le rapport Q de Dixon risquent de ne pas être efficaces.
- Si vous ne savez pas si vos données comprennent des valeurs aberrantes, utilisez le test de Grubb.
- Si vous savez que vos données comprennent une valeur aberrante ou plus, utilisez l'un des tests de Dixon. Les tests de Dixon sont conçus pour surpasser l'effet de masque que plusieurs valeurs aberrantes peuvent causer.
Dans l'illustration suivante, chaque colonne montre comment les différents test de rapport de Dixon traitent un même échantillon. La valeur entourée est la valeur potentiellement aberrante. Les X indiquent les valeurs de données que chaque test de rapport de Dixon ignore lorsqu'il calcule la statistique de test. (Cette illustration suppose que l'hypothèse alternative est soit La valeur la plus petite ou la plus grande est une valeur aberrante, soit La valeur la plus grande est une valeur aberrante.) Pour ces données, le test de rapport de Dixon r22 a plus de chances d'identifier la valeur entourée comme aberrante.
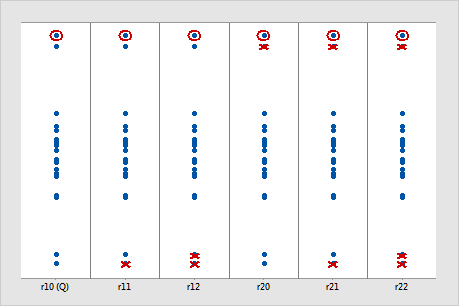
Des échantillons plus importants pour une population normale risquent davantage de comporter des valeurs extrêmes. Dixon a proposé les consignes générales suivantes pour les rapports.
| Effectif d'échantillon (n) | Rapport recommandé |
|---|---|
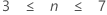 |
r10 (aussi appelé rapport Q de Dixon) |
 |
r11 |
 |
r21 |
 |
r22 |
Seuil de signification
Comparez le seuil de signification à la valeur de p pour décider s'il faut rejeter ou non l'hypothèse nulle (H0). Si la valeur de p est inférieure au seuil de signification, l'interprétation est généralement que les résultats sont statistiquement significatifs, et vous rejetez H0.
- Choisissez un seuil de signification plus important, tel que 0,10, pour être sûr de détecter toutes les différences qui puissent exister. Par exemple, un ingénieur qualité compare la stabilité de nouveaux roulements à billes à celle des roulements existants. Il doit s'assurer que les nouveaux roulements à billes sont absolument stables car, si ce n'est pas le cas, ils pourraient provoquer une catastrophe. L'ingénieur choisit un seuil de signification de 0,10 afin d'augmenter sa certitude de détecter toute différence possible dans la stabilité des roulements à billes.
- Choisissez un seuil de signification moins important, tel que 0,01, pour être sûr de détecter uniquement une différence existant réellement. Par exemple, un scientifique travaillant pour une entreprise pharmaceutique doit s'assurer de la véracité de l'affirmation selon laquelle le nouveau médicament de l'entreprise réduit significativement les symptômes. Il choisit un seuil de signification de 0,001 afin d'augmenter sa certitude qu'il existe une différence significative dans les symptômes.
Que souhaitez-vous déterminer ? (Hypothèse alternative)
- La valeur la plus petite ou la plus grande est une valeur aberrante : Utilisez ce test bilatéral lorsque la valeur minimale ou maximale peut être une valeur aberrante. Ce test bilatéral peut détecter des valeurs aberrantes pour la valeur minimale ou maximale, mais il est moins puissant qu'un test unilatéral.
- La valeur la plus petite est une valeur aberrante : Utilisez ce test unilatéral lorsque vous soupçonnez que la valeur minimale est une valeur aberrante. Ce test unilatéral est plus puissant qu'un test bilatéral, mais il ne peut pas détecter les valeurs aberrantes correspondant à la valeur maximale.
- La valeur la plus grande est une valeur aberrante : Utilisez ce test unilatéral lorsque vous soupçonnez que la valeur maximale est une valeur aberrante. Ce test unilatéral est plus puissant qu'un test bilatéral, mais il ne peut pas détecter les valeurs aberrantes correspondant à la valeur minimale.
