Méthodes et formules pour la fonction Test des valeurs aberrantes

Par exemple, si la valeur aberrante soupçonnée est la plus petite valeur de l'échantillon, mais que celui-ci comprend également deux valeurs inhabituellement grandes, alors r₁₂ est la statistique de test adaptée. La statistique de test r₁₀ (aussi appelée test Q de Dixon) est adaptée lorsque l'échantillon comprend seulement une valeur extrême.

Les valeurs critiques pour les statistiques de test de Dixon sont tabulées d'après Rorabacher (1991).

Statistiques de test unilatéral

La formule du test unilatéral varie selon que vous testiez la plus petite valeur, y_i, ou la plus grande, y_n. Pour tester si y_i est la valeur aberrante, utilisez la formule suivante :

Pour tester si y_n est la valeur aberrante, utilisez la formule suivante :

Statistiques de test bilatéral

Nous définissons la statistique de test bilatéral comme la définit King (1953) par rapport à r₁₀. La statistique de test bilatéral s'obtient comme suit :

Notation

Références

Formule pour la statistique unilatérale

Si vous effectuez ce test pour savoir si la valeur de la plus petite donnée est aberrante, le calcul de la statistique de test G se fait comme suit :

Si vous effectuez ce test pour savoir si la valeur de la plus grande donnée est aberrante, G se calcule comme suit :

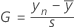
Formule pour la statistique bilatérale

Pour une hypothèse bilatérale, G s'obtient comme suit :

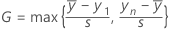
Notation

Terme	Description
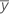	moyenne de l'échantillon
yi	ie plus petite valeur de l'échantillon
s	écart type de l'échantillon
n	nombre d'observations dans l'échantillon

Fonction de distribution cumulée pour la statistique de test

D'après Dixon (1951) et McBane (2006), les fonctions de densité de probabilité de la distribution des statistiques de test r_ij peuvent s'écrire comme suit :

où C est le facteur de normalisation obtenu par :

et le jacobien J(x,v,r) est obtenu par :

Si l'on utilise la transformation où t = (1 + r² ) v² / 2 et u² = 3x² / 2, la fonction de densité peut s'écrire comme suit :

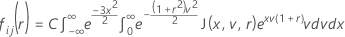
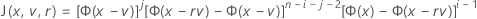
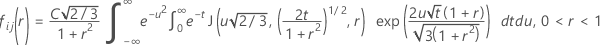
Minitab évalue l'entier interne à l'aide d'une quadrature à 30 points de Gauss-Laguerre. Minitab évalue l'entier externe à l'aide d'une quadrature à 30 points de Gauss-Laguerre.

Les fonctions de distribution cumulée de la famille de statistiques de test s'obtient comme suit :

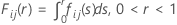
Comme McBane (2006), Minitab calcule F_ij(r) à l'aide de la méthode de quadrature à 16 points de Gauss-Laguerre.

Valeur de p pour le test unilatéral

Pour toute paire d'indices (i, j), la valeur de p pour la statistique unilatérale observée s'obitent comme suit :

Valeur de p pour le test unilatéral

Si l'on utilise le résultat de King (1953), pour toute paire d'indices (i, j), la valeur de p pour la statistique bilatérale observée, r, s'obtient comme suit :

Par ailleurs, King observe que l'approximation ci-dessus devient une égalité pour .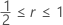

Notation

Références

W. J. Dixon (1951), "Ratios Involving Extreme Values", Annals of Mathematical Statistics, 22(1), 68-78.

E. P. King (1953), "On Some Procedures for the Rejection of Suspected Data", Journal of the American Statistical Association, vol. 48, No. 263, pages 531-533.

G. C. McBane (2006), "Programs to Compute Distribution Functions and Critical Values for Extreme Value Ratios for Outlier Detection", Journal of Statistical Software, vol. 16, No. 3, pages 1-9.

Formule pour un test unilatéral

La valeur de p pour un test unilatéral est :

Formule pour un test bilatéral

La valeur de p pour un test bilatéral est :

Valeurs de p exactes ou approximatives

Si ce qui suit est vrai, alors la valeur de p est exacte.

Dans le cas contraire, la valeur de p calculée représente une borne supérieure pour la valeur de p exacte. Cependant, la borne supérieure donne une très bonne idée de la valeur exacte de p.

Notation