Sur ce thème
Hypothèse nulle et hypothèse alternative
- Hypothèse nulle
- L'hypothèse nulle indique que toutes les valeurs de données obéissent à la même loi de distribution normale.
- Hypothèse alternative
- L'hypothèse alternative indique que la plus petite ou la plus grande valeur des données est une valeur aberrante.
Seuil de signification
Le seuil de signification (noté alpha ou α) est le niveau maximal acceptable du risque de rejet de l'hypothèse nulle lorsqu'elle est vraie (erreur de type I). La valeur par défaut est 0,05.
Interprétation
Utilisez le seuil de signification pour déterminer si l'hypothèse nulle (H0) doit être rejetée. Si la probabilité qu'un événement se produise est inférieure au seuil de signification, l'interprétation est généralement que les résultats sont statistiquement significatifs, et vous rejetez H0.
- Choisissez un seuil de signification plus important, tel que 0,10, pour être sûr de détecter toutes les différences qui puissent exister. Par exemple, un ingénieur qualité compare la stabilité de nouveaux roulements à billes à celle des roulements existants. Il doit s'assurer que les nouveaux roulements à billes sont absolument stables car, si ce n'est pas le cas, ils pourraient provoquer une catastrophe. L'ingénieur choisit un seuil de signification de 0,10 afin d'augmenter sa certitude de détecter toute différence possible dans la stabilité des roulements à billes.
- Choisissez un seuil de signification moins important, tel que 0,01, pour être sûr de détecter uniquement une différence existant réellement. Par exemple, un scientifique travaillant pour une entreprise pharmaceutique doit s'assurer de la véracité de l'affirmation selon laquelle le nouveau médicament de l'entreprise réduit significativement les symptômes. Il choisit un seuil de signification de 0,001 afin d'augmenter sa certitude qu'il existe une différence significative dans les symptômes.
N
L'effectif de l'échantillon (N) est le nombre d'observations total de l'échantilon.
Interprétation
L'effectif de l'échantillon affecte la puissance du test.
En général, un effectif d'échantillon plus grand donne au test plus de puissance pour détecter une valeur aberrante. Pour plus d'informations, reportez-vous à la rubrique Qu'est-ce que la puissance ?.
Moyenne
Elle est calculée comme la moyenne des données, c'est-à-dire la somme de toutes les observations, divisée par le nombre d'observations.
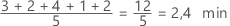
Interprétation
Utilisez la moyenne pour décrire l'échantillon avec une seule valeur qui représente le centre des données. De nombreuses analyses statistiques utilisent la moyenne en tant que mesure standard pour le centre de la loi des données.
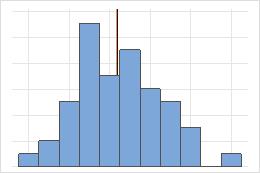
Symétrique
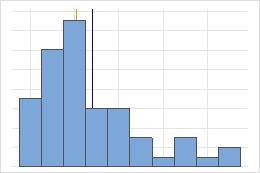
Non symétrique
Pour la loi symétrique, la moyenne (ligne bleue) et la médiane (ligne orange) sont tellement proches qu'il est difficile de distinguer les deux lignes. Toutefois, la loi non symétrique présente un asymétrie vers la droite.
EcTyp
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données sur la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit.
Etant donné que l'écart type utilise les mêmes unités que les données, il est généralement plus facile à interpréter que la variance.
Interprétation
Utilisez l'écart type pour déterminer la dispersion des données par rapport à la moyenne. Une valeur d'écart type élevée indique que les données sont dispersées. D'une manière générale, pour une loi normale, environ 68 % des valeurs se situent dans un écart type de la moyenne, 95 % des valeurs se situent dans deux écarts types et 99,7 % des valeurs se situent dans trois écarts types.
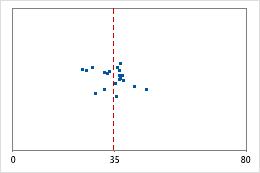
Hôpital 1
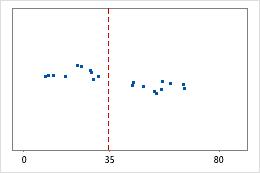
Hôpital 2
Durée jusqu'à la sortie de l'hôpital
Les administrateurs de deux hôpitaux étudient le temps que passent les patients dans le service des urgences de leurs établissements jusqu'à leur sortie. Bien que ces durées moyennes soient pratiquement identiques (35 minutes), les écarts types diffèrent de manière significative. L'écart type pour l'hôpital 1 est d'environ 6. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 6 minutes par rapport à la moyenne (ligne bleue). L'écart type pour l'hôpital 2 est d'environ 20. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 20 minutes par rapport à la moyenne (ligne bleue).
Maximum
Le maximum est la valeur de la donnée la plus importante.
Dans ces données, le maximum est 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le maximum pour identifier une éventuelle valeur aberrante ou une erreur d'entrée de données. L'une des manières les plus simples d'estimer la dispersion de vos données consiste à comparer le minimum et le maximum. Si la valeur maximale est très élevée, même en tenant compte du centre, de la répartition et de la forme des données, recherchez la cause de cette valeur extrême.
Minimum
Le minimum est la valeur de données la plus petite.
Dans ces données, le minimum est de 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le minimum pour identifier une éventuelle valeur aberrante ou une erreur d'entrée de données. L'une des manières les plus simples d'estimer la répartition de vos données consiste à comparer le minimum et le maximum. Si la valeur minimum est très basse, même en tenant compte du centre, de la répartition et de la forme des données, recherchez la cause de cette valeur extrême.
Valeur aberrante
Une valeur aberrante est une observation inhabituellement élevée ou basse. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales).
Ligne
Ligne de la feuille de travail contenant la valeur aberrante. Minitab affiche cette valeur uniquement lorsqu'elle est aberrante.
x[i] et x[N-i]
Lorsque vous utilisez l'un des tests de rapport de Dixon, Minitab affiche plus d'observations dans le tableau de test, en plus du minimum et du maximum. La valeur entre parenthèses indique la taille de l'observation par rapport aux autres valeurs. Par exemple, x[2] représente la 2e plus petite observation, et x[N-1] représente la 2e plus grande observation.
G
La statistique de test de Grubb (G) est la différence entre la moyenne de l'échantillon et la valeur de donnée la plus petite ou la plus grande, divisé par l'écart type. Minitab utilise la statistique de test de Grubb pour calculer la valeur de p, c'est-à-dire la probabilité de rejeter une hypothèse nulle quand elle est vraie.
P
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Une valeur de p inférieure fournit des preuves plus solides par rapport à l'hypothèse nulle.
Interprétation
Utilisez la valeur de p pour déterminer la présence d'une valeur aberrante.
- Valeur de p ≤ α : il existe une valeur aberrante (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et conclure qu'il existe une valeur aberrante. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Envisagez de supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales).
- Valeur de p > α : vous ne pouvez pas conclure qu'il existe une valeur aberrante (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle, car vous ne possédez pas suffisamment de preuves pour conclure qu'il existe une valeur aberrante. Vous devez vous assurer que votre test est assez puissant pour détecter une valeur aberrante. Pour plus d'informations, reportez-vous à la rubrique Augmentation de la puissance.
Diagramme des valeurs aberrantes
Un diagramme des valeurs aberrantes est similaire à un diagramme des valeurs individuelles. Utilisez le diagramme des valeurs aberrantes pour repérer visuellement une valeur aberrante dans les données. Si les données contiennent une valeur aberrante, Minitab la représente par un carré rouge sur le diagramme. Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales).
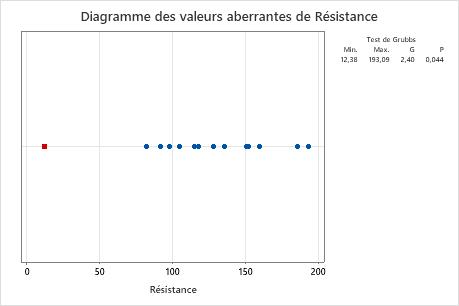
Dans ces résultats, la plus petite valeur, 12,38, est aberrante.
