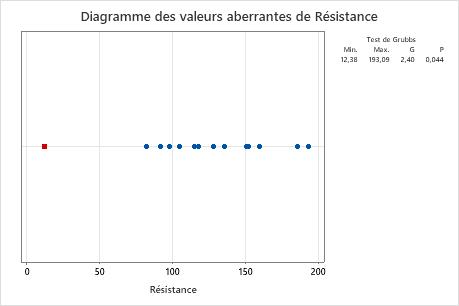
Un ingénieur qualité d'une entreprise fabriquant des manches à balai en bois teste la résistance d'un échantillon aléatoire. Il note la force requise pour briser chaque manche à balai. Il crée un graphique des données et remarque que l'une des valeurs de l'échantillon semble anormalement petite.
L'ingénieur exécute un test des valeurs aberrantes pour déterminer si la plus petite valeur est une valeur aberrante.
- Ouvrez le fichier de données échantillons, RésistanceManche.MWX.
- Sélectionnez .
- Dans la zone Variables, saisissez Résistance.
- Cliquez sur Options.
- Dans la fonction Que souhaitez-vous déterminer ? (Hypothèse alternative), sélectionnez La valeur la plus petite est une valeur aberrante.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
La moyenne de l'échantillon est de 123,4. La statistique G indique que la valeur de donnée la plus petite, 12,38, est inférieure de 2,4 écarts types à la moyenne. La valeur de p indique que, si toutes les valeurs proviennent réellement de la même population normalement distribuée, la probabilité d'obtenir une si petite valeur minimale n'est que de 0,044. Comme la valeur de p de 0,044 est inférieure au seuil de signification (appelé α ou alpha) de 0,05, l'ingénieur rejette l'hypothèse nulle et conclut que la plus petite valeur est une valeur aberrante.
L'ingénieur recherche la cause et découvre que la personne ayant saisi les données a accidentellement tapé 12,28 au lieu de 123,8.
Méthode
| Hypothèse nulle | Toutes les valeurs proviennent de la même population normale |
|---|---|
| Hypothèse alternative | La valeur la plus petite est une valeur aberrante |
| Seuil de signification | α = 0,05 |
Test de Grubbs
| Variable | N | Moyenne | EcTyp | Min. | Max. | G | P |
|---|---|---|---|---|---|---|---|
| Résistance | 14 | 123,4 | 46,3 | 12,4 | 193,1 | 2,40 | 0,044 |
Valeur aberrante
| Variable | Ligne | Valeur aberrante |
|---|---|---|
| Résistance | 10 | 12,38 |