Moyenne
La moyenne décrit l'échantillon avec une seule valeur, qui représente le centre des données. Elle est calculée comme la moyenne des données, c'est-à-dire la somme de toutes les observations, divisée par le nombre d'observations.
N
L'effectif de l'échantillon (N) est le nombre d'observations total de l'échantilon.
Interprétation
L'effectif de l'échantillon affecte la puissance du test.
Généralement, un effectif d'échantillon plus important rend le test plus puissant pour détecter une différence entre vos données échantillons et la distribution normale. C'est-à-dire que lorsqu'une différence existe réellement, vous avez de plus grandes chances de la détecter si l'effectif de l'échantillon est important.
EcTyp
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données par rapport à la moyenne. Un écart type d'échantillon supérieur indique que vos données sont réparties plus largement autour de la moyenne.
AD
La statistique d'ajustement d'Anderson-Darling (AD) mesure l'aire comprise entre la ligne ajustée (qui correspond à la loi normale) et la fonction de répartition empirique (qui correspond aux points de données). La statistique d'Anderson-Darling est le carré d'une distance ayant une pondération plus élevée aux extrémités de la loi de distribution.
Interprétation
Minitab utilise la statistique d'Anderson-Darling pour calculer la valeur de p. La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Une valeur de p inférieure fournit des preuves plus solides par rapport à l'hypothèse nulle. Des valeurs plus importantes pour la statistique d'Anderson-Darling indiquent que les données ne suivent pas la loi de distribution normale.
KS
Le test de Kolmogorov-Smirnov compare la fonction de répartition empirique (ECDF) des données échantillons à la loi de distribution qui pourrait être attendue si les données étaient normales.
Interprétation
Minitab utilise la statistique de Kolmogorov-Smirnov pour calculer la valeur de p. La valeur de p correspond à la probabilité d'obtenir une statistique de test (telle que la statistique de Kolmogorov-Smirnov) au moins aussi extrême que la valeur que vous avez calculée à partir de l'échantillon, lorsque les données sont normales. Des valeurs plus importantes pour la statistique de Kolmogorov-Smirnov indiquent que les données ne suivent pas la loi de distribution normale.
RJ
La statistique de Ryan-Joiner mesure l'ajustement des données à une loi de distribution normale en calculant la corrélation entre vos données et leurs scores normaux. Si le coefficient de corrélation est proche de 1, la population est susceptible d'être normale. Ce test est semblable au test de normalité de Shapiro-Wilk.
Interprétation
Minitab utilise la statistique de Ryan-Joiner pour calculer la valeur de p. La valeur de p correspond à la probabilité d'obtenir une statistique de test (telle que la statistique de Ryan-Joiner) au moins aussi extrême que la valeur que vous avez calculée à partir de l'échantillon, lorsque les données sont normales. Des valeurs plus importantes pour la statistique de Ryan-Joiner indiquent que les données ne suivent pas la loi de distribution normale.
Valeur de p
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Une valeur de p inférieure fournit des preuves plus solides par rapport à l'hypothèse nulle.
Interprétation
Utilisez la valeur de p pour déterminer si les données ne suivent pas la loi normale.
- Valeur de p ≤ α : les données ne suivent pas une loi normale (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et en conclure que vos données ne suivent pas une loi normale.
- Valeur de p > α : vous ne pouvez pas conclure que les données ne suivent pas une loi normale (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que les données ne suivent pas une loi normale
Diagramme de probabilité
Une diagramme de probabilité crée, à partir de l'échantillon, une fonction de répartition cumulée (CDF) estimée en traçant la valeur de chaque observation par rapport à sa probabilité cumulée estimée.
Interprétation
Utilisez un diagramme de probabilité pour déterminer dans quelle mesure vos données suivent une loi normale.
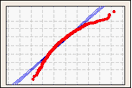
Données asymétriques vers la droite
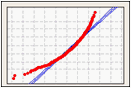
Données asymétriques vers la gauche
Conseil
Dans Minitab, maintenez le curseur sur la droite de distribution ajustée pour afficher le graphique des percentiles et des valeurs.
