Sur ce thème
Etape 1 : Décrire le centre des données
Utilisez la moyenne pour décrire l'échantillon avec une seule valeur qui représente le centre des données. De nombreuses analyses statistiques utilisent la moyenne en tant que mesure standard pour le centre de la loi des données.
La médiane est une autre mesure du centre de la loi. Elle est généralement moins influencée par les valeurs aberrantes que la moyenne. La moitié des valeurs de données est supérieure à la valeur de la médiane, tandis que l'autre moitié des valeurs est inférieure.
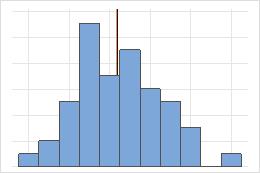
Symétrique
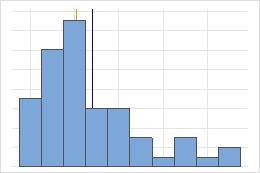
Non symétrique
Pour la loi symétrique, la moyenne (ligne bleue) et la médiane (ligne orange) sont tellement proches qu'il est difficile de distinguer les deux lignes. Toutefois, la loi non symétrique présente un asymétrie vers la droite.
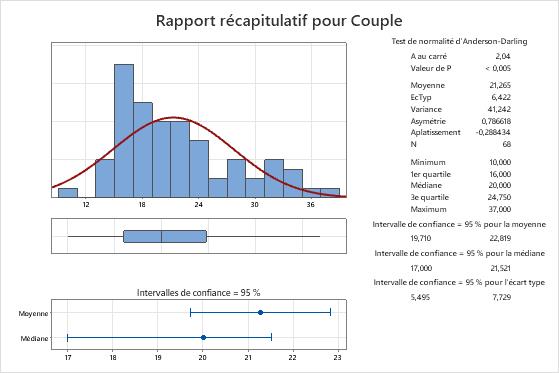
Résultats principaux : moyenne et médiane
Dans ces résultats, le couple moyen requis pour retirer un bouchon d'un tube de dentifrice est de 21,265, et le couple médian est de 20. Les données semblent asymétriques à droite, ce qui explique pourquoi la moyenne est supérieure à la médiane.
Etape 2 : Déterminer un intervalle de confiance pour la moyenne, la médiane et l'écart type
L'intervalle de confiance fournit une étendue de valeurs probables pour le paramètre de population. Par exemple, un niveau de confiance de 95 % indique que, sur 100 échantillons pris de façon aléatoire parmi la population, environ 95 de ces échantillons devraient produire des intervalles contenant le paramètre de population.

Résultats principaux : intervalle de confiance pour la moyenne, intervalle de confiance pour la médiane, intervalle de confiance pour EcTyp
- La moyenne de la population pour les mesures de couples est comprise entre 19,710 et 22,819.
- La médiane de la population pour les mesures de couples est comprise entre 17 et 21,521.
- L'écart type de la population pour les mesure de couples est compris entre 5,495 et 7,729.
Etape 3 : Evaluer à la forme et à la répartition de votre loi de distribution des données
Utilisez l'histogramme et la boîte à moustaches pour évaluer la forme et la répartition des données, et pour identifier toute éventuelle valeur aberrante.
Examen de la répartition des données pour déterminer si elles semblent asymétriques.
Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
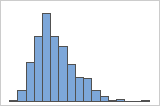
Asymétrie à droite
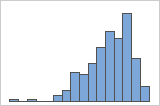
Asymétrie à gauche
L'histogramme avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. L'histogramme avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
Identification des valeurs aberrantes
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
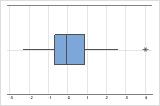
Sur une boîte à moustaches, les astérisques (*) indiquent les valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
Recherche de données multimodales
Les données multimodales présentent plusieurs pics, également appelés modes. Les données multimodales indiquent souvent que des variables importantes ne sont pas encore représentées.
Si des informations supplémentaires vous permettent de classer les observations en groupes, vous pouvez créer une variable de groupe avec ces informations. Vous pouvez ensuite créer le graphique avec des groupes pour déterminer si la variable de groupe explique les pics dans les données.
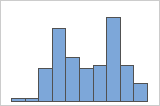
Simple
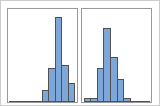
Avec groupes
Par exemple, un responsable de banque collecte des données de temps d'attente et crée un histogramme simple. L'histogramme présente deux pics. Après examen, le responsable détermine que le temps d'attente est plus court pour les clients qui encaissent des chèques que pour ceux qui font des demandes de prêt sur valeur domiciliaire. Le responsable ajoute une variable de groupe pour la tâche client, puis crée un histogramme avec des groupes.
