Interprétation des résultats principaux pour la fonction Test d'ajustement de Poisson

Suivez la procédure ci-dessous pour interpréter un test d'ajustement de Poisson. Les résultats principaux comprennent la valeur de p et plusieurs graphiques.

Sur ce thème

Etape 1 : Déterminer si les données ne respectent pas la loi de Poisson
Etape 2 : Examiner la différence entre les valeurs observées et attendues pour chaque catégorie

Etape 1 : Déterminer si les données ne respectent pas la loi de Poisson

Pour déterminer si les données ne suivent pas une loi de Poisson, comparez la valeur de p à votre seuil de signification (α). En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique un risque de 5 % de conclure que les données ne suivent pas une loi de Poisson alors qu'elles la suivent.

Valeur de p ≤ α : les données ne suivent pas une loi de Poisson (Rejeter H₀): Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et en conclure que vos données ne suivent pas une loi de Poisson.
Valeur de p > α : vous ne pouvez pas conclure que les données ne suivent pas une loi de Poisson (Impossible de rejeter H₀): Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle, car vous n'êtes pas en mesure de conclure que les données ne suivent pas une loi de Poisson.

Méthode

Effectifs dans Observé

Statistiques descriptives

N	Moyenne
300	0,536667

Dénombrements observés et attendus pour Défauts

Défauts	Probabilité de Poisson	Dénombrement observé	Dénombrement attendu	Contribution au Khi deux
0	0,584694	213	175,408	8,056
1	0,313786	41	94,136	29,993
2	0,084199	18	25,260	2,086
>=3	0,017321	28	5,196	100,072

Test du Khi deux

Hypothèse nulle	H₀ : les données suivent une loi de Poisson
Hypothèse alternative	H₁ : les données ne suivent pas une loi de Poisson

DL	Khi deux	Valeur de P
2	140,208	0,000

Résultat principal : valeur de p

Dans ces résultats, l'hypothèse nulle indique que les données suivent la loi de Poisson. La valeur de p étant de 0,000, ce qui est inférieur à 0,05, il faut rejeter l'hypothèse nulle. Vous pouvez conclure que les données ne respectent pas la loi de Poisson.

Etape 2 : Examiner la différence entre les valeurs observées et attendues pour chaque catégorie

Utilisez une carte barre de valeurs observées et attendues pour déterminer, pour chaque catégorie, si le nombre de valeurs observées est différent du nombre de valeurs attendues. Des différences importantes entre les valeurs observées et attendues indiquent que les données ne suivent pas une distribution de Poisson.

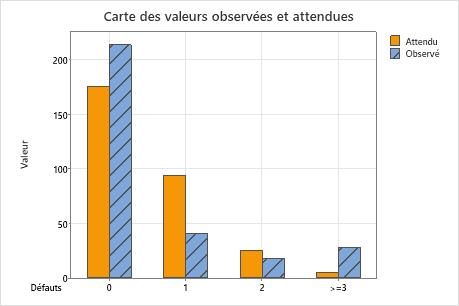
Cette carte barre indique que les valeurs observées pour 0 défaut, 1 défaut et plus de 3 défauts sont différentes des valeurs attendues. Ainsi, la carte barre confirme visuellement ce qui est indiqué par la valeur de p, à savoir que les données ne suivent pas une loi Poisson.