Un ingénieur qualité d'une société d'appareils électroniques de grande consommation souhaite savoir si la distribution des défauts par téléviseur obéit à une loi de Poisson. Il sélectionne 300 postes de télévision de manière aléatoire et enregistre le nombre de défauts par poste.
- Ouvrez le fichier de données échantillons, DéfautsTéléviseur.MTW.
- Sélectionnez .
- Dans la zone Variable, saisissez Défauts.
- Dans la zone Variable d'effectif : (facultatif), saisissez Observé.
- Cliquez sur OK.
Interprétation des résultats
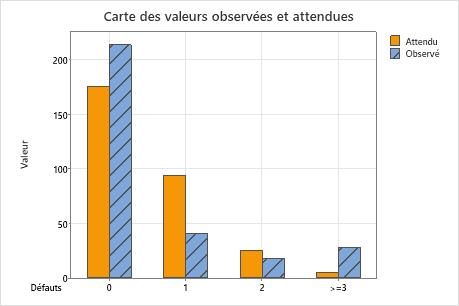
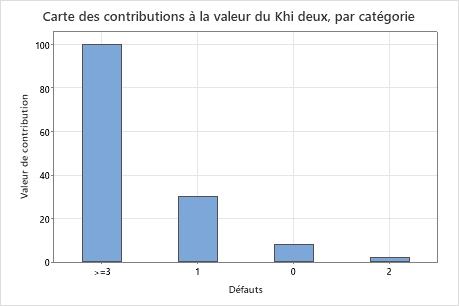
L'hypothèse nulle indique que les données suivent la loi de Poisson. La valeur de p de 0,000 étant inférieure au seuil de signification de 0,05, l'ingénieur rejette l'hypothèse nulle et conclut que les données ne suivent pas une distribution de Poisson. Le graphique indique que la différence entre les valeurs observées et attendues est importante pour les catégories 1 et 
3, et que la catégorie 3 est celle qui contribue le plus à la statistique du Khi deux.
Méthode
| Effectifs dans Observé |
|---|
Statistiques descriptives
| N | Moyenne |
|---|---|
| 300 | 0,536667 |
Dénombrements observés et attendus pour Défauts
| Défauts | Probabilité de Poisson | Dénombrement observé | Dénombrement attendu | Contribution au Khi deux |
|---|---|---|---|---|
| 0 | 0,584694 | 213 | 175,408 | 8,056 |
| 1 | 0,313786 | 41 | 94,136 | 29,993 |
| 2 | 0,084199 | 18 | 25,260 | 2,086 |
| >=3 | 0,017321 | 28 | 5,196 | 100,072 |
Test du Khi deux
| Hypothèse nulle | H₀ : les données suivent une loi de Poisson |
|---|---|
| Hypothèse alternative | H₁ : les données ne suivent pas une loi de Poisson |
| DL | Khi deux | Valeur de P |
|---|---|---|
| 2 | 140,208 | 0,000 |
