Sur ce thème
Boîte à moustaches
Une boîte à moustaches fournit un récapitulatif graphique de la loi de distribution d'un échantillon. La boîte à moustaches indique la forme, la tendance centrale et la variabilité des données.
Interprétation
Utilisez une boîte à moustaches pour examiner la dispersion des données et pour détecter d'éventuelles valeurs aberrantes. Les boîtes à moustaches sont plus adaptées lorsque l'effectif d'échantillon est supérieur à 20.
- Données asymétriques
-
Examinez de la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
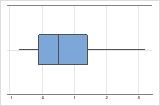
Asymétrie à droite
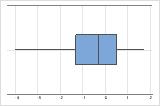
Asymétrie à gauche
La boîte à moustaches avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. La boîte à moustaches avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
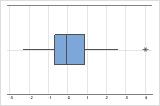
Sur une boîte à moustaches, les astérisques (*) indiquent les valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
Histogramme
Un histogramme divise les valeurs des échantillons en plusieurs intervalles et représente l'effectif des valeurs contenues dans chaque intervalle par une barre.
Interprétation
Utilisez un histogramme pour évaluer la forme et la dispersion des données. Les histogrammes sont plus adaptés lorsque l'effectif d'échantillon est supérieur à 20.
- Données asymétriques
-
Vous pouvez utiliser un histogramme des données avec courbe normale pour évaluer la normalité de vos données. Une loi normale est symétrique et en forme de cloche. Il est souvent difficile d'évaluer la normalité avec de petits échantillons. Un diagramme de probabilité est le meilleur moyen de déterminer l'ajustement de la loi.
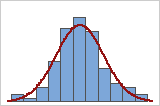
Ajustement correct
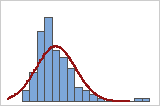
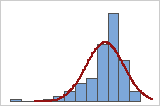
Ajustement incorrect
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
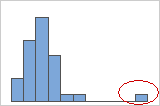
Sur un histogramme, des barres isolées à une extrémité ou l'autre du graphique indiquent de possibles valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
- Données multimodales
-
Les données multimodales présentent plusieurs pics, également appelés modes. Les données multimodales indiquent souvent que des variables importantes ne sont pas encore représentées.
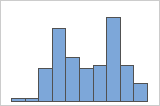
Simple
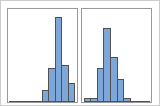
Avec groupes
Par exemple, un responsable de banque collecte des données de temps d'attente et crée un histogramme simple. L'histogramme présente deux pics. Après examen, le responsable détermine que le temps d'attente est plus court pour les clients qui encaissent des chèques que pour ceux qui font des demandes de prêt sur valeur domiciliaire. Le responsable ajoute une variable de groupe pour la tâche client, puis crée un histogramme avec des groupes.
Si des informations supplémentaires vous permettent de classer les observations en groupes, vous pouvez créer une variable de groupe avec ces informations. Vous pouvez ensuite créer le graphique avec des groupes pour déterminer si la variable de groupe explique les pics dans les données.
Diagramme des valeurs individuelles
Un diagramme des valeurs individuelles présente les valeurs individuelles contenues dans l'échantillon. Chaque cercle représente une observation. Un diagramme des valeurs individuelles est particulièrement utile lorsque vous disposez de relativement peu d'observations et que vous avez besoin d'évaluer l'effet de chacune d'entre elles.
Interprétation
Utilisez un diagramme des valeurs individuelles pour examiner la dispersion des données et pour détecter d'éventuelles valeurs aberrantes. Les diagrammes des valeurs individuelles sont plus adaptés lorsque l'effectif d'échantillon est inférieur à 50.
- Données asymétriques
-
Examinez de la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
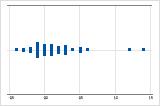
Asymétrie à droite
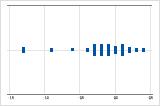
Asymétrie à gauche
Le diagramme des valeurs individuelles avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. Le diagramme des valeurs individuelles avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
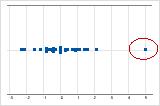
Sur un diagramme des valeurs individuelles, les valeurs de données anormalement élevées ou faibles indiquent de possibles valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
Q1
Les quartiles sont les trois valeurs—le premier quartile à 25 % (Q1), le deuxième quartile à 50 % (Q2 ou médian) et le troisième quartile à 75 % (Q3)—qui divisent un échantillon de données ordonnées en quatre parts égales.
Le premier quartile est le 25e percentile et indique que 25 % des données sont inférieures ou égales à cette valeur.
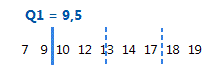
Pour ces données ordonnées, le premier quartile (Q1) est 9,5. C'est-à-dire que 25 % des données sont inférieures ou égales à 9,5.
EIQ
L'étendue interquartile (EIQ) est la distance entre le premier quartile (Q1) et le troisième quartile (Q3). 50 % des données sont dans cette étendue.

Pour ces données ordonnées, l'étendue interquartile est 8 (17,5–9,5 = 8). C'est-à-dire que les 50 % des données situées au milieu se trouvent entre 9,5 et 17,5.
Interprétation
Utilisez l'étendue interquartile pour décrire la répartition des données. A mesure que la répartition des données augmente, l'EIQ devient plus important.
Maximum
Le maximum est la valeur de la donnée la plus importante.
Dans ces données, le maximum est 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le maximum pour identifier une éventuelle valeur aberrante ou une erreur d'entrée de données. L'une des manières les plus simples d'estimer la dispersion de vos données consiste à comparer le minimum et le maximum. Si la valeur maximale est très élevée, même en tenant compte du centre, de la répartition et de la forme des données, recherchez la cause de cette valeur extrême.
Médiane
La médiane représente le milieu de l'ensemble de données. Ce point de milieu est celui qui sépare les observations en deux moitiés égales, l'une supérieure à la valeur, l'autre inférieure. La médiane est déterminée en classant les observations, puis en prenant l'observation de rang [N + 1] / 2 dans l'ordre obtenu. Si le nombre d'observations est pair, la médiane est égale à la moyenne des observations de rang N/2 et [N/2] + 1.
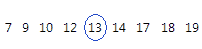
Pour les données ordonnées ci-dessous, la médiane est 13. Autrement dit, la moitié des valeurs est inférieure ou égale à 13 et l'autre moitié est supérieure ou égale à 13. Si vous ajoutez une autre observation égale à 20, la médiane est de 13,5, soit la moyenne entre la 5e observation (13) et la 6e observation (14).
Interprétation
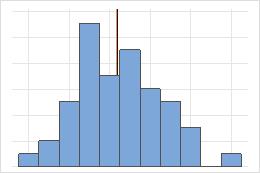
Symétrique
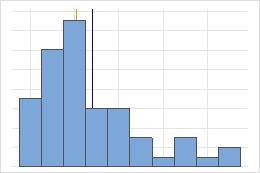
Non symétrique
Pour la loi symétrique, la moyenne (ligne bleue) et la médiane (ligne orange) sont tellement proches qu'il est difficile de distinguer les deux lignes. Toutefois, la loi non symétrique présente un asymétrie vers la droite.
Minimum
Le minimum est la valeur de données la plus petite.
Dans ces données, le minimum est de 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le minimum pour identifier une éventuelle valeur aberrante ou une erreur d'entrée de données. L'une des manières les plus simples d'estimer la répartition de vos données consiste à comparer le minimum et le maximum. Si la valeur minimum est très basse, même en tenant compte du centre, de la répartition et de la forme des données, recherchez la cause de cette valeur extrême.
Etendue
L'étendue est la différence entre la plus grande valeur des données de l'échantillon et la plus petite. L'étendue représente l'intervalle contenant l'ensemble des valeurs des données.
Interprétation
Utilisez l'étendue pour comprendre l'importance de la dispersion des données. Une valeur d'étendue importante indique une plus grande dispersion des données. Une petite valeur d'étendue indique que les données sont moins dispersées. Comme l'étendue est calculée à l'aide de seulement deux valeurs de données, elle est plus utile avec de petits fichiers de données.
Q3
Les quartiles sont les trois valeurs (le premier quartile à 25 % (Q1), le deuxième quartile à 50 % (Q2 ou médiane) et le troisième quartile à 75 % (Q3)) qui divisent un échantillon de données ordonnées en quatre parts égales.
Le troisième quartile est le 75e percentile et indique que 75 % des données sont inférieures ou égales à cette valeur.
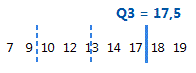
Pour ces données ordonnées, le troisième quartile (Q3) est 17,5. C'est-à-dire que 75 % des données sont inférieures ou égales à 17,5.
Moyenne
Elle est calculée comme la moyenne des données, c'est-à-dire la somme de toutes les observations, divisée par le nombre d'observations.
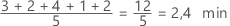
Interprétation
Utilisez la moyenne pour décrire l'échantillon avec une seule valeur qui représente le centre des données. De nombreuses analyses statistiques utilisent la moyenne en tant que mesure standard pour le centre de la loi des données.

Symétrique

Non symétrique
Pour la loi symétrique, la moyenne (ligne bleue) et la médiane (ligne orange) sont tellement proches qu'il est difficile de distinguer les deux lignes. Toutefois, la loi non symétrique présente un asymétrie vers la droite.
ErT moyenne
L'erreur type de la moyenne (ErT moyenne) estime la variabilité entre les moyennes d'échantillons que vous obtiendriez si vous preniez des échantillons répétés de la même population. Elle évalue la variabilité d'un échantillon à un autre, tandis que l'écart type mesure la variabilité au sein d'un même échantillon.
Par exemple, vous disposez d'un délai de livraison moyen de 3,80 jours avec un écart type de 1,43 jour, basé sur un échantillon aléatoire de 312 délais de livraison. Ces chiffres génèrent une erreur type de la moyenne de 0,08 jour (1,43 divisé par la racine carrée de 312). Si vous prenez en compte plusieurs échantillons aléatoires de même effectif et provenant de la même population, l'écart type de ces différentes moyennes d'échantillons tournerait autour de 0,08 jour.
Interprétation
Vous pouvez utiliser l'erreur type de la moyenne pour déterminer avec quelle précision la moyenne de l'échantillon évalue la moyenne de la population.
Lorsque la valeur de l'erreur type de la moyenne est moins élevée, l'estimation de la moyenne de la population est plus précise. En règle générale, plus l'écart type est grand, plus l'erreur type de la moyenne est élevée et moins l'estimation de la moyenne de la population est précise. En revanche, plus l'effectif d'échantillon est élevé, plus l'erreur type de la moyenne est faible et plus l'estimation de la moyenne de la population est précise.
Minitab utilise l'erreur type de la moyenne pour calculer l'intervalle de confiance.
MoyTronquée
La moyenne des données, à l'exclusion des 5 % de valeurs les plus élevées et des 5 % de valeurs les moins élevées.
La moyenne tronquée permet d'éliminer l'impact des valeurs très élevées ou très faibles sur la moyenne. Lorsque les données comportent des valeurs aberrantes, la moyenne tronquée peut s'avérer être une meilleure mesure de la tendance centrale que la moyenne.
NCum
| Niveau scolaire | Dénombrement | NCum | Calcul |
|---|---|---|---|
| 1 | 49 | 49 | 49 |
| 2 | 58 | 107 | 49 + 58 |
| 3 | 52 | 159 | 49 + 58 + 52 |
| 4 | 60 | 219 | 49 + 58 + 52 + 60 |
| 5 | 48 | 267 | 49 + 58 + 52 + 60 + 48 |
| 6 | 55 | 322 | 49 + 58 + 52 + 60 + 48 + 55 |
N*
Nombre de valeurs manquantes dans votre échantillon. Le nombre de valeurs manquantes correspond au nombre de cellules contenant le symbole de valeur manquante *.
| Dénombrement total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N
Nombre de valeurs présentes dans votre échantillon.
| Dénombrement total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Dénombrement total
Nombre total d'observations dans la colonne. Sert à représenter le total des valeurs présentes et manquantes.
| Dénombrement total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
%Cum
Le pourcentage cumulé est la somme des pourcentages pour chaque groupe de la colonne Variable de répartition. Dans l'exemple suivant, la colonne Variable de répartition contient 4 groupes : Ligne 1, Ligne 2, Ligne 3 et Ligne 4.
| Groupe (variable de répartition) | Pourcentage | %Cum |
|---|---|---|
| Chaîne 1 | 16 | 16 |
| Chaîne 2 | 20 | 36 |
| Chaîne 3 | 36 | 72 |
| Chaîne 4 | 28 | 100 |
Pourcentage
Le pourcentage d'observations dans chaque groupe Par variable. Dans l'exemple suivant, il y a quatre groupes : Ligne 1, Ligne 2, Ligne 3 et Ligne 4.
| Groupe (par variable) | Pourcentage |
|---|---|
| Chaîne 1 | 16 |
| Chaîne 2 | 20 |
| Chaîne 3 | 36 |
| Chaîne 4 | 28 |
Aplatissement
L'aplatissement indique dans quelle mesure les queues d'une loi diffèrent de la loi normale.
Interprétation
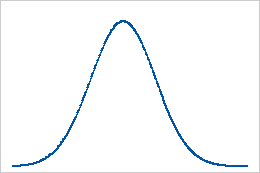
Référence : valeur d'aplatissement de 0
La loi normale sert de référence pour l'aplatissement. Une valeur d'applatissement de 0 indique que les données suivent parfaitement la loi de distribution normale. Une valeur d'aplatissement déviant significativement de la valeur 0 peut indiquer que les données ne sont pas distribuées normalement.
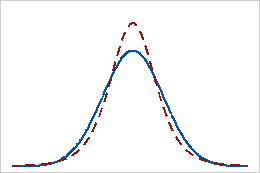
Aplatissement positif
Les données possédant une valeur d'aplatissement positive présentent des queues plus lourdes qu'avec la loi normale. Par exemple, les données qui suivent une loi t ont une valeur d'aplatissement positive. La ligne continue représente la loi normale et la ligne en pointillés représente une loi possédant une valeur d'aplatissement positive.
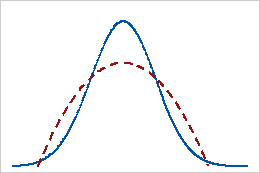
Aplatissement négatif
Les données ayant une valeur d'aplatissement négative présentent des queues plus légères qu'avec la loi normale. Par exemple, les données qui suivent une loi bêta avec un premier et un deuxième paramètres de forme égaux à 2 ont une valeur d'aplatissement négative. La ligne continue représente la loi normale et la ligne en pointillés représente une loi possédant une valeur d'aplatissement négative.
Asymétrie
L'asymétrie évalue dans quelle mesure vos données ne sont pas symétriques.
Interprétation
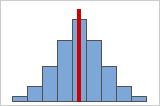
Figure A
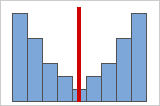
Figure B
Distributions symétriques ou non asymétriques
Plus des données sont symétriques, plus leur valeur d'asymétrie approche de zéro. La figure A montre des données distribuées normalement qui, par définition, présentent une asymétrie relativement faible. Si vous traciez une ligne verticale au milieu de cet histogramme de données normales, vous pourriez facilement constater que les deux côtés se reflètent l'un l'autre. Toutefois, l'absence d'asymétrie n'est pas en soi synonyme de normalité. La figure B représente une loi de distribution dont les deux côtés se reflètent également, mais les données sont loin d'être distribuées normalement.
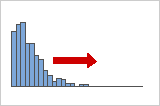
Distributions positives ou asymétriques à droite
Les données présentant une asymétrie positive ou asymétriques à droite doivent leur appellation au fait que la "queue" de la loi de distribution pointe vers la droite et que leur valeur d'asymétrie est supérieure à 0 (ou est positive). Les données salariales présentent souvent une asymétrie de ce type : au sein d'une entreprise, de nombreux employés gagnent relativement peu et, à mesure que les salaires augmentent, le nombre d'employés concernés diminue.
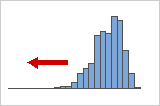
Distributions négatives ou asymétriques à gauche
Les données asymétriques à gauche ou présentant une asymétrie négative doivent leur nom au fait que la "queue" de leur loi de distribution pointe vers la gauche et qu'elles génèrent une valeur d'asymétrie négative. Les données sur les taux de défaillance sont souvent asymétriques à gauche. Prenez par exemple le cas d'ampoules électriques : très peu vont griller immédiatement, la très grande majorité ayant une durée de vie assez longue.
VarCoeff
Le coefficient de variation (appelé CDV) est une mesure de la répartition qui décrit la variation des données par rapport à la moyenne. Le coefficient de variation s'ajuste de sorte que les valeurs soient sur une échelle sans unités. C'est pourquoi vous pouvez utiliser le coefficient de variation à la place de l'écart type pour comparer la variation des données ayant des unités ou des moyennes très différentes.
Interprétation
Plus le coefficient de variation est élevé, plus les données sont dispersées.
| Grande brique | Petite brique |
|---|---|
| CDV = 100 * 0,4 tasses / 16 tasses = 2,5 | CDV = 100 * 0,08 tasses / 1 tasse = 8 |
EcTyp
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données sur la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit.
Etant donné que l'écart type utilise les mêmes unités que les données, il est généralement plus facile à interpréter que la variance.
Interprétation
Utilisez l'écart type pour déterminer la dispersion des données par rapport à la moyenne. Une valeur d'écart type élevée indique que les données sont dispersées. D'une manière générale, pour une loi normale, environ 68 % des valeurs se situent dans un écart type de la moyenne, 95 % des valeurs se situent dans deux écarts types et 99,7 % des valeurs se situent dans trois écarts types.
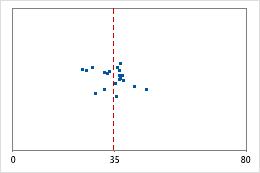
Hôpital 1
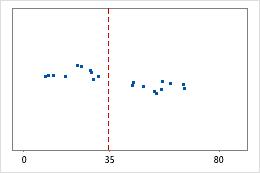
Hôpital 2
Durée jusqu'à la sortie de l'hôpital
Les administrateurs de deux hôpitaux étudient le temps que passent les patients dans le service des urgences de leurs établissements jusqu'à leur sortie. Bien que ces durées moyennes soient pratiquement identiques (35 minutes), les écarts types diffèrent de manière significative. L'écart type pour l'hôpital 1 est d'environ 6. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 6 minutes par rapport à la moyenne (ligne bleue). L'écart type pour l'hôpital 2 est d'environ 20. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 20 minutes par rapport à la moyenne (ligne bleue).
Variance
La variance mesure le degré de dispersion des données autour de leur moyenne. Elle est égale à l'écart type au carré.
Interprétation
Plus la variance est élevée, plus les données sont dispersées.
Etant donné que la variance (σ2) représente une quantité élevée au carré, ses unités sont également élevées au carré. C'est pourquoi la variance est difficile à utiliser dans la pratique. Il est généralement plus facile d'interpréter l'écart type, car il utilise les mêmes unités que les données. Par exemple, un échantillon de temps d'attente à un arrêt de bus peut avoir une moyenne de 15 minutes et une variance de 9 minutes2. Etant donné que la variance n'utilise pas les mêmes unités que les données, elle est généralement affichée avec sa racine carrée, l'écart type. Une variance de 9 minutes2 est équivalente à un écart type de 3 minutes.
Mode
Le mode est la valeur la plus fréquente dans un ensemble d'observations. Minitab affiche également le nombre de points de données égaux au mode.
La moyenne et la médiane nécessitent un calcul, mais le mode implique seulement le décompte du nombre d'occurrences de chaque valeur dans un ensemble de données.
Interprétation
Vous pouvez utiliser le mode avec la moyenne et la médiane pour fournir une caractérisation globale de la distribution des données. Vous pouvez également utiliser le mode pour identifier des problèmes dans vos données.
Par exemple, une loi de distribution comptant plus d'un mode peut détecter que votre échantillon comprend des données de deux populations. Si les données contiennent deux modes, la loi de distribution est bimodale. Si les données contiennent plus de deux modes, la loi de distribution est multimodale.
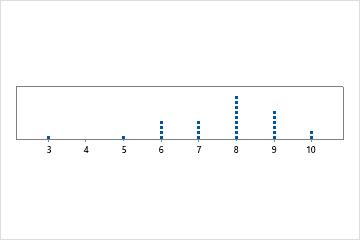
Unimodale
Il n'existe qu'un mode le plus fréquent, 8.
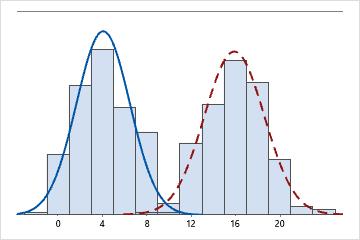
Bimodale
Il existe deux modes, 4 et 16. Il semble que les données représentent deux populations différentes.
Moitié de la moyenne du carré des différences successives (MMCDS)
La MSSD est la moyenne des différences successives carrées. La MSSD est une estimation de la variance. Elle peut être utilisée pour tester si une séquence d'observations est aléatoire. En contrôle qualité, la MSSD peut être utilisée pour estimer la variance lorsque l'effectif du sous-groupe est égal à 1.
Somme
La somme est le total de toutes les valeurs des données. La somme est également utilisée dans les calculs statistiques, comme la moyenne et l'écart type.
Somme des carrés
La somme non corrigée des carrés se calcule en mettant au carré chaque valeur de la colonne, et en calculant la somme de ces valeurs au carré. Par exemple, si la colonne contient x1, x2, ... , xn, la somme des carrés est égale à (x12 + x22 + ... + xn2). A la différence de la somme des carrés corrigée, la somme des carrés non corrigée inclut l'erreur. Les valeurs sont élevées au carré sans soustraction préalable de la moyenne.
