Sur ce thème
Etape 1 : Examiner les relations entre les variables d'un graphique matriciel diagonal
Utilisez le diagramme matriciel diagonal pour examiner les relations entre deux variables continues. Vérifiez également qu'il n'y ait pas de valeurs aberrantes dans les relations. Les valeurs aberrantes peuvent considérablement influer sur le coefficient de corrélation de Pearson dans les résultats.
Déterminez si les relations sont linéaires, monotones ou ni l'un ni l'autre. Voici des exemples des types de formes que décrivent les coefficients de corrélation. Le coefficient de corrélation de Pearson convient aux formes linéaires. Le coefficient de corrélation de Spearman convient aux formes monotones.

Aucune relation
Les points sont placés de façon aléatoire dans le diagramme, ce qui indique qu'il n'existe aucune relation linéaire entre les variables.
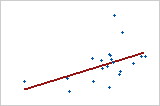
Relation modérément positive
Certains points sont proches de la ligne, mais d'autres en sont éloignés, ce qui indique seulement une relation linéaire modérée entre les variables.
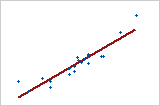
Relation largement positive
Les points sont proches de la ligne, ce qui indique qu'il existe une forte relation linéaire entre les variables. La relation est positive, car lorsqu'une variable augmente, l'autre augmente également.
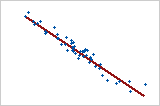
Relation largement négative
Les points sont proches de la ligne, ce qui indique qu'il existe une forte relation négative entre les variables. La relation est négative, car lorsqu'une variable augmente, l'autre décroit.
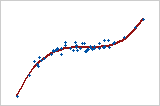
Monotone
Dans une relation monotone, les variables ont tendance à se déplacer dans la même direction relative, mais pas forcément à une vitesse constante. Dans une relation linéaire, les variables se déplacent dans la même direction, à une vitesse constante. Ce diagramme montre que les deux variables augmentent simultanément, mais pas à la même vitesse. Cette relation est monotone, mais pas linéaire. Le coefficient de corrélation de Pearson pour ces données est 0,843, mais celui de la corrélation de Spearman est plus élevé, 0,948.
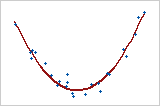
Courbe quadratique
Cet exemple illustre une relation en courbe. Même si la relation entre les variables est forte, le coefficient de corrélation serait proche de zéro. La relation n'est ni linéaire ni monotone.
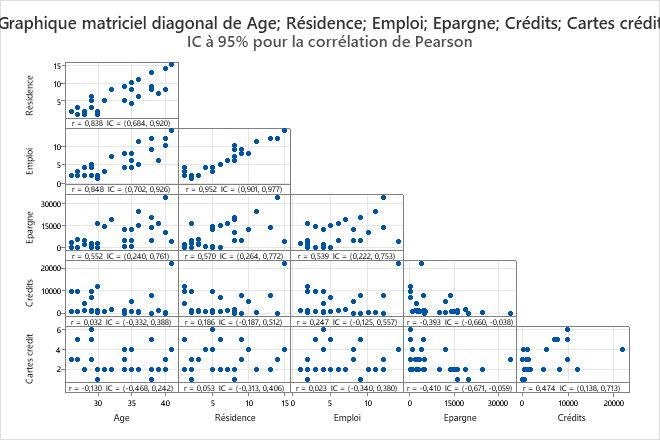
Résultat principal : diagramme matriciel diagonal
- Une forte relation linéaire positive existe entre les variables Emploi et Résidence.
- Une faible relation linéaire négative existe entre les variables Cartes crédit et Epargne.
- Crédits semble avoir une valeur aberrante, ce qu'il faudra étudier.
Etape 2 : Examiner les coefficients de corrélation entre les variables
Utilisez le coefficient de corrélation de Pearson pour examiner la puissance et la direction de la relation linéaire qui existe entre deux variables continues.
- Force
-
Le coefficient de corrélation peut avoir une valeur comprise entre -1 et +1. Plus la valeur absolue du coefficient est importante, plus la relation linéaire entre les variables est forte.
Pour la corrélation de Pearson, une valeur absolue de 1 indique une relation linéaire parfaite. Une corrélation proche de 0 indique l'absence de relation linéaire entre les variables. - Sens
-
Le signe du coefficient indique la direction de la relation. Si les deux variables ont tendance à augmenter ou à diminuer ensemble, le coefficient est positif et la ligne qui représente la corrélation est ascendante. Si une variable tend à augmenter tandis que l'autre diminue, la corrélation est négative et la ligne qui la représente est descendante.
- Il est impossible de conclure que des modifications dans une variable provoquent des modifications dans une autre à partir d'une corrélation seule. Seules des expériences correctement contrôlées vous permettent de déterminer si une relation est causale.
- Le coefficient de corrélation de Pearson est très sensible aux valeurs de données extrêmes. Une seule valeur très différente des autres dans un fichier de données peut modifier de façon significative la valeur du coefficient. Vous devrez déterminer la cause de toute valeur extrême. Corrigez les erreurs de mesure ou d’entrée des données. Pensez éventuellement à supprimer les valeurs de données associées à des événements anormaux et uniques (causes spéciales). Ensuite, répétez l'analyse.
- Un faible coefficient de corrélation de Pearson ne signifie pas qu'aucune relation n'existe entre les variables. Les variables peuvent avoir une relation non linéaire.
Méthode
| Type de corrélation | Pearson |
|---|---|
| Nombre de lignes utilisées | 30 |
Corrélation
| Age | Résidence | Emploi | Epargne | Crédits | |
|---|---|---|---|---|---|
| Résidence | 0,838 | ||||
| Emploi | 0,848 | 0,952 | |||
| Epargne | 0,552 | 0,570 | 0,539 | ||
| Crédits | 0,032 | 0,186 | 0,247 | -0,393 | |
| Cartes crédit | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
Résultat principal : corrélation de Pearson
- Résidence et Age, 0,838
- Emploi et Age, 0,848
- Emploi et Résidence, 0,952
- Crédits et Epargne, −0,393
- Cartes crédit et Age, −0,130
- Cartes crédit et Epargne, −0,410
