Sur ce thème
Corrélations de Pearson
La matrice de corrélation indique les valeurs de corrélation, qui mesurent le degré de relation linéaire entre chaque paire de variables. Les valeurs de corrélation peuvent être comprises entre -1 et +1. Si les deux variables ont tendance à augmenter et à diminuer en même temps, la valeur de corrélation est positive. Lorsqu'une variable augmente alors que l'autre diminue, la valeur de corrélation est négative.
Interprétation
Utilisez la matrice de corrélation pour évaluer l'importance et la direction de la relation entre deux variables. Une valeur de corrélation positive élevée indique que les variables mesurent la même caractéristique. Si les items ne sont pas fortement corrélés, ils peuvent mesurer des caractéristiques différentes ou ne pas être clairement définis.
Corrélation
| Age | Résidence | Emploi | Epargne | Crédits | |
|---|---|---|---|---|---|
| Résidence | 0,838 | ||||
| Emploi | 0,848 | 0,952 | |||
| Epargne | 0,552 | 0,570 | 0,539 | ||
| Crédits | 0,032 | 0,186 | 0,247 | -0,393 | |
| Cartes crédit | -0,130 | 0,053 | 0,023 | -0,410 | 0,474 |
- Résidence et Age, 0,838
- Emploi et Age, 0,848
- Emploi et Résidence, 0,952
- Crédits et Epargne, −0,393
- Cartes crédit et Age, −0,130
- Cartes crédit et Epargne, −0,410
Corrélations de Spearman
Utilisez le coefficient de corrélation de Spearman pour examiner l'importance et la direction de la relation monotone entre deux variables continues ou ordinales. Dans une relation monotone, les variables ont tendance à se déplacer dans la même direction relative, mais pas forcément à une vitesse constante. Pour calculer la corrélation de Spearman, Minitab classe les données brutes. Ensuite, Minitab calcule le coefficient de corrélation selon les données classées.
- Force
-
Le coefficient de corrélation peut avoir une valeur comprise entre -1 et +1. Plus la valeur absolue du coefficient est importante, plus la relation linéaire entre les variables est forte.
Pour la corrélation de Spearman, une valeur absolue de 1 indique que les données classées par ligne sont parfaitement linéaires. Par exemple, une corrélation de Spearman de -1 signifie que la valeur la plus élevée de la Variable A est associée à la valeur la plus basse de la Variable B ; la deuxième valeur la plus élevée de la Variable A est associée à la deuxième valeur la plus basse de la Variable B, et ainsi de suite.
- Sens
-
Le signe du coefficient indique la direction de la relation. Si les deux variables ont tendance à augmenter ou à diminuer ensemble, le coefficient est positif et la ligne qui représente la corrélation est ascendante. Si une variable tend à augmenter tandis que l'autre diminue, la corrélation est négative et la ligne qui la représente est descendante.
Les diagrammes suivants montrent les données avec les valeurs des coefficients de corrélation de Spearman pour illustrer les différents schémas d'importance et de direction des relations entre les variables.

Aucune relation : rang de Spearman = 0
Les points sont placés de façon aléatoire dans le diagramme, ce qui indique qu'il n'existe aucune relation entre les variables.
Forte relation positive : rang de Spearman = 0,948
Les points sont proches de la ligne, ce qui indique qu'il existe une forte relation entre les variables. La relation est positive car les variables augmentent simultanément.

Forte relation négative : rang de Spearman = -1,0
Les points sont proches de la ligne, ce qui indique qu'il existe une forte relation entre les variables. La relation est négative car lorsqu'une variable augmente, l'autre décroit.
Il est impossible de conclure que des modifications dans une variable provoquent des modifications dans une autre à partir d'une corrélation seule. Seules des expériences correctement contrôlées vous permettent de déterminer si une relation est causale.
Interprétation
Corrélation
| Age | Résidence | Emploi | Epargne | Crédits | |
|---|---|---|---|---|---|
| Résidence | 0,824 | ||||
| Emploi | 0,830 | 0,912 | |||
| Epargne | 0,570 | 0,571 | 0,496 | ||
| Crédits | -0,198 | -0,142 | -0,056 | -0,605 | |
| Cartes crédit | -0,179 | 0,069 | 0,036 | -0,480 | 0,353 |
Corrélations de Spearman deux à deux
| Echantillon 1 | Echantillon 2 | N | Corrélation | IC à 95% pour ρ | Valeur de P |
|---|---|---|---|---|---|
| Résidence | Age | 30 | 0,824 | (0,624; 0,922) | 0,000 |
| Emploi | Age | 30 | 0,830 | (0,636; 0,926) | 0,000 |
| Epargne | Age | 30 | 0,570 | (0,236; 0,783) | 0,001 |
| Crédits | Age | 30 | -0,198 | (-0,524; 0,178) | 0,293 |
| Cartes crédit | Age | 30 | -0,179 | (-0,508; 0,197) | 0,345 |
| Emploi | Résidence | 30 | 0,912 | (0,798; 0,963) | 0,000 |
| Epargne | Résidence | 30 | 0,571 | (0,237; 0,784) | 0,001 |
| Crédits | Résidence | 30 | -0,142 | (-0,479; 0,232) | 0,454 |
| Cartes crédit | Résidence | 30 | 0,069 | (-0,300; 0,419) | 0,719 |
| Epargne | Emploi | 30 | 0,496 | (0,144; 0,737) | 0,005 |
| Crédits | Emploi | 30 | -0,056 | (-0,408; 0,311) | 0,768 |
| Cartes crédit | Emploi | 30 | 0,036 | (-0,328; 0,392) | 0,849 |
| Crédits | Epargne | 30 | -0,605 | (-0,804; -0,283) | 0,000 |
| Cartes crédit | Epargne | 30 | -0,480 | (-0,726; -0,124) | 0,007 |
| Cartes crédit | Crédits | 30 | 0,353 | (-0,020; 0,639) | 0,056 |
Dans ces résultats, la corrélation de Spearman entre les variables Résidence et Age est de 0,824, ce qui indique une relation positive entre les variables. L'intervalle de confiance pour rhô s'étend de 0,624 à 0,922. La valeur de p est égale à 0,000, ce qui indique que la relation est statistiquement significative au niveau de α = 0,05.
La corrélation de Spearman entre Crédits et Epargne est de –0,605, et entre Cartes crédit et Epargne, de –0,480. La relation entre ces variables est négative, ce qui indique que lorsque Crédits et Cartes crédit augmentent, Epargne diminue.
Lignes utilisées
Le nombre de lignes utilisées s'affiche dans le tableau Méthode. Il s'agit du nombre de lignes de données qui comprennent des valeurs manquantes.
En cas de valeurs manquantes, le nombre de lignes utilisées ne correspond pas à l'effectif d'échantillon réellement utilisé dans le calcul de l'intervalle de confiance.
Intervalles de confiance pour les corrélations
L'intervalle de confiance fournit une étendue de valeurs probables pour les coefficients de corrélation. Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Toutefois, si vous répétiez l'échantillonnage de nombreuses fois, un certain pourcentage des intervalles de confiance ou des bornes obtenus contiendrait le coefficient de corrélation inconnu. Le pourcentage de ces intervalles de confiance ou des bornes contenant le coefficient de corrélation est le niveau de confiance de l'intervalle.
Par exemple, un niveau de confiance de 95 % indique que, sur 100 échantillons pris de façon aléatoire parmi la population, environ 95 devraient produire des intervalles contenant le coefficient de corrélation.
Une borne supérieure définit une valeur à laquelle la différence de la population est susceptible d'être inférieure. Une borne inférieure définit une valeur à laquelle la différence de la population est susceptible d'être supérieure.
Les intervalles de confiance pour la corrélation de Pearson sont sensibles à la normalité de la loi bivariée sous-jacente. Si les données s'écartent de la normalité, les intervalles de confiance peuvent être inexacts, quel que soit l'effectif de l'échantillon.
Les intervalles de confiance pour les corrélations de Spearman reposent sur des rangs et sont moins sensibles à l'hypothèse de la loi bivariée sous-jacente.
Interprétation
L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon. Pour plus d'informations, reportez-vous à la rubrique Obtenir un intervalle de confiance plus précis.
Corrélations de Pearson deux à deux
| Echantillon 1 | Echantillon 2 | N | Corrélation | IC à 95% pour ρ | Valeur de P |
|---|---|---|---|---|---|
| Résidence | Age | 30 | 0,838 | (0,684; 0,920) | 0,000 |
| Emploi | Age | 30 | 0,848 | (0,702; 0,926) | 0,000 |
| Epargne | Age | 30 | 0,552 | (0,240; 0,761) | 0,002 |
| Crédits | Age | 30 | 0,032 | (-0,332; 0,388) | 0,865 |
| Cartes crédit | Age | 30 | -0,130 | (-0,468; 0,242) | 0,494 |
| Emploi | Résidence | 30 | 0,952 | (0,901; 0,977) | 0,000 |
| Epargne | Résidence | 30 | 0,570 | (0,264; 0,772) | 0,001 |
| Crédits | Résidence | 30 | 0,186 | (-0,187; 0,512) | 0,326 |
| Cartes crédit | Résidence | 30 | 0,053 | (-0,313; 0,406) | 0,779 |
| Epargne | Emploi | 30 | 0,539 | (0,222; 0,753) | 0,002 |
| Crédits | Emploi | 30 | 0,247 | (-0,125; 0,557) | 0,189 |
| Cartes crédit | Emploi | 30 | 0,023 | (-0,340; 0,380) | 0,906 |
| Crédits | Epargne | 30 | -0,393 | (-0,660; -0,038) | 0,032 |
| Cartes crédit | Epargne | 30 | -0,410 | (-0,671; -0,059) | 0,024 |
| Cartes crédit | Crédits | 30 | 0,474 | (0,138; 0,713) | 0,008 |
Dans ces résultats, Age et Résidence ont une corrélation linéaire positive égale à 0,838. Vous pouvez être sûr à 95 % que le coefficient de corrélation de la population est compris entre 0,684 et 0,920. Souvent, plus la corrélation est élevée, plus l'intervalle de confiance est étroit. Par exemple, Cartes crédit et Age ont une faible corrélation et l'intervalle de confiance à 95 % est compris entre –0,468 et 0,242.
Valeur de p
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Une valeur de p inférieure permet d'invalider l'hypothèse nulle avec plus de certitude.
Interprétation
Utilisez la valeur de p afin de déterminer si le coefficient de corrélation est statistiquement significatif.
- Valeur de p ≤ α : la corrélation est statistiquement significative (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle. Vous pouvez en conclure que la corrélation est statistiquement significative. Utilisez vos connaissances afin de déterminer si la différence est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Signification statistique et pratique.
- Valeur de p > α : la corrélation n'est pas statistiquement significative (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que la corrélation est statistiquement significative.
Les procédures relatives à la valeur de p pour la corrélation de Pearson et pour la corrélation de Spearman sont robustes aux écarts par rapport à la normalité. Les valeurs de p sont généralement exactes pour n ≥ 25, indépendamment de la population parente de l'échantillon.
Corrélations de Pearson deux à deux
| Echantillon 1 | Echantillon 2 | N | Corrélation | IC à 95% pour ρ | Valeur de P |
|---|---|---|---|---|---|
| Résidence | Age | 30 | 0,838 | (0,684; 0,920) | 0,000 |
| Emploi | Age | 30 | 0,848 | (0,702; 0,926) | 0,000 |
| Epargne | Age | 30 | 0,552 | (0,240; 0,761) | 0,002 |
| Crédits | Age | 30 | 0,032 | (-0,332; 0,388) | 0,865 |
| Cartes crédit | Age | 30 | -0,130 | (-0,468; 0,242) | 0,494 |
| Emploi | Résidence | 30 | 0,952 | (0,901; 0,977) | 0,000 |
| Epargne | Résidence | 30 | 0,570 | (0,264; 0,772) | 0,001 |
| Crédits | Résidence | 30 | 0,186 | (-0,187; 0,512) | 0,326 |
| Cartes crédit | Résidence | 30 | 0,053 | (-0,313; 0,406) | 0,779 |
| Epargne | Emploi | 30 | 0,539 | (0,222; 0,753) | 0,002 |
| Crédits | Emploi | 30 | 0,247 | (-0,125; 0,557) | 0,189 |
| Cartes crédit | Emploi | 30 | 0,023 | (-0,340; 0,380) | 0,906 |
| Crédits | Epargne | 30 | -0,393 | (-0,660; -0,038) | 0,032 |
| Cartes crédit | Epargne | 30 | -0,410 | (-0,671; -0,059) | 0,024 |
| Cartes crédit | Crédits | 30 | 0,474 | (0,138; 0,713) | 0,008 |
Dans ces résultats, de nombreuses valeurs de p sont inférieures au seuil de signification de 0,05, ce qui indique que les coefficients de la corrélation de Pearson sont statistiquement significatifs.
Remarque
Dans certains cas, à cause de points de données extrêmes, la valeur de p peut être faible, mais l'intervalle de confiance très large. Par exemple, avec les variables Crédits et Cartes crédit, l'IC à 95 % est très large, mais la valeur de p est faible. Lorsque vous observez le graphique matriciel diagonal, vous pouvez voir un point de donnée extrême.
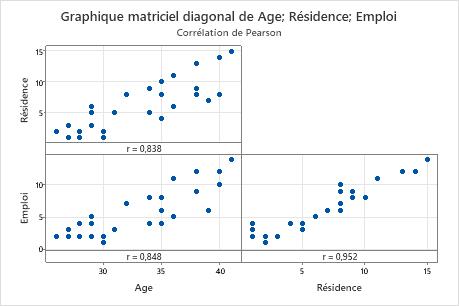
Graphique matriciel diagonal
Un graphique matriciel diagonal est un ensemble de nuages de points. Chaque nuage de points de la matrice représente les scores correspondant à une paire d'items sur les axes x et y.
Interprétation
Utilisez le graphique pour évaluer visuellement la relation entre chaque combinaison de variables. Les relations peuvent être linéaires, monotones ou ni l'un ni l'autre. Le diagramme matriciel diagonal vous permet également de voir les valeurs aberrantes qui peuvent considérablement influer sur les résultats. Pour plus d'informations sur les types de relations, reportez-vous à la rubrique Diagrammes de relations linéaires, non linéaires et monotones.
Le graphique matriciel diagonal suggère que toutes les paires d'items ont une relation linéaire positive.