Sur ce thème
- Statistiques d'échantillons
- Test pour la méthode de Bonett avec des plans équilibrés
- Test pour la méthode de Bonett avec des plans non équilibrés
- Intervalle de confiance pour la méthode de Bonett
- Test pour la méthode de Levene
- Intervalles de confiance pour la méthode de Levene
- Test pour la méthode de test F
- Intervalles de confiance pour la méthode du test F
Statistiques d'échantillons
Formule
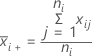
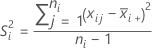
Notation
| Terme | Description |
|---|---|
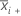 | moyenne de l'échantillon i |
| S2i | variance de l'échantillon i |
| Xij | je mesure du ie échantillon |
| ni | effectif de l'échantillon i |
Test pour la méthode de Bonett avec des plans équilibrés
Formule pour la statistique de test
Lorsque n1 = n2 , la statistique de test est Z2. Si l'hypothèse nulle, ρ = ρ0 est vraie, alors Z2 est distribué selon la loi de Khi deux avec 1 degré de liberté. Z2 s'obtient comme suit :
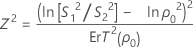
où ErT(ρ0) est l'erreur type de l'aplatissement regroupé, qui s'obtient comme suit :
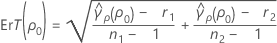
où ri = ( ni - 3) / ni et 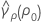 est l'aplatissement regroupé, qui s'obtient comme suit :
est l'aplatissement regroupé, qui s'obtient comme suit :
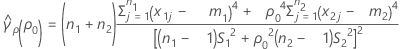
ErT2(ρ0) peut également s'exprimer en termes de valeurs d'aplatissement de chaque échantillon, 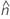 , comme suit :
, comme suit :
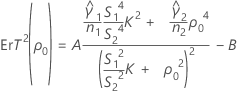
où :
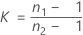

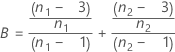
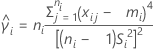
Formule pour la valeur de p
Si z2 est la valeur de Z2 obtenue à partir des données. Dans l'hypothèse nulle, H0 : ρ = ρ0 , Z est distribué selon la loi de distribution normale standard. Donc, les valeurs de p pour les hypothèses alternatives (H1) s'obtiennent comme suit.
| Hypothèse | Valeur de p |
|---|---|
| H1 : ρ0 ≠ ρ0 | P = 2P(Z > |z|) |
| H1: ρ0 > ρ0 | P = P(Z > z) |
| H1 : ρ0 < ρ0 | P = P(Z < z) |
Notation
| Terme | Description |
|---|---|
| Si | écart type de l'échantillon i |
| ρ | rapport des écarts types de la population |
| ρ0 | rapport hypothétisé des écarts types de la population |
| α | seuil de signification pour le test = 1 - (niveau de confiance / 100) |
| ni | nombre d'observations dans l'échantillon i |
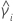 | valeur de l'aplatissement pour l'échantillon i |
| Xij | je observation de l'échantillon i |
| mi | moyenne tronquée pour l'échantillon i avec des proportions de troncage de  |
Test pour la méthode de Bonett avec des plans non équilibrés
Formule
Lorsque n1 ≠ n2 , il n'existe aucune statistique de test. En revanche, la valeur de p est calculée en inversant la procédure de l'intervalle de confiance. La valeur de p pour le test s'obtient comme suit :
P = 2 min (αL, αU)
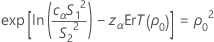
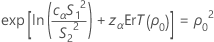
où cα est une constante égalisatrice décrite ci-dessous et ErT(ρ0) est l'erreur type pour l'aplatissement regroupé, qui s'obtient comme suit :
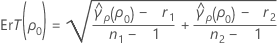
où ri = (ni - 3) / ni et 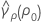 est l'aplatissement regroupé, qui s'obtient comme suit :
est l'aplatissement regroupé, qui s'obtient comme suit :
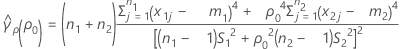
ErT(ρ0) peut également s'exprimer en termes de valeurs d'aplatissement de chaque échantillon. Pour plus d'informations, consultez la section consacrée au test pour la méthode de Bonett avec des plans équilibrés.
Constante égalisatrice
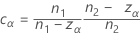
La constante disparaît lorsque les plans sont équilibrés et son effet devient négligeable lorsque les effectifs d'échantillons augmentent.
Trouver αL et αU
Trouver αL et αU équivaut à trouver les zéros des fonctions L(z , n1 , n2 , S1 , S2 ) et L(z , n2 , n1 , S2 , S1 ), où L(z , n1 , n2 , S1 , S2) s'obtient comme suit :
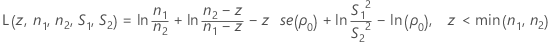
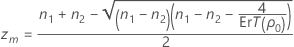
- Calculez zm et évaluez L(z, n1, n2, S1, S2).
- Si L(zm)
 0, trouvez le zéro zL, de L(z, n1, n2, S1, S2) dans l'intervalle
0, trouvez le zéro zL, de L(z, n1, n2, S1, S2) dans l'intervalle  et calculez αL = P( Z > zL).
et calculez αL = P( Z > zL). - Si L(zm) > 0, alors la fonction L(z , n1, n2, S1, S2) n'a pas de zéro, et αL = 0.
- Si L(zm)
- Calculez L(0, n1, n2, S1, S2) = Dans (S12 / S22).
- Si L(0, n1, n2, S1, S2)
 0, puis trouvez le zéro z0, de L(z, n1, n2, S1, S2) dans l'intervalle [0, n2).
0, puis trouvez le zéro z0, de L(z, n1, n2, S1, S2) dans l'intervalle [0, n2). - Si L(0, n1, n2, S1, S2) < 0, trouvez le zéro zL dans l'intervalle
 .
.
- Si L(0, n1, n2, S1, S2)
- Calculez αL = P( Z > zL).
Pour calculer αU, effectuez les étapes précédentes en utilisant la fonction L(z, n2, n1, S2, S1), au lieu de la fonction L(z, n1, n2, S1, S2).
Notation
| Terme | Description |
|---|---|
| Si | écart type de l'échantillon i |
| ρ | rapport des écarts types de la population |
| ρ0 | rapport hypothétisé des écarts types de la population |
| α | seuil de signification pour le test = 1 - (niveau de confiance / 100) |
| zα | point de percentile supérieur α de la loi normale standard |
| ni | nombre d'observations dans l'échantillon i |
| Xij | je observation de l'échantillon i |
| mi | moyenne tronquée pour l'échantillon i avec des proportions de troncage de  |
Intervalle de confiance pour la méthode de Bonett
Formule
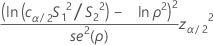
où cα/2 est une constante égalisatrice (décrite ci-dessous) et ErT(ρ) est l'erreur type pour l'aplatissement regroupé (décrit ci-dessous). Généralement, cette équation a deux solutions : L < S1 / S2, et U > S1 / S2. L est la limite de confiance la plus basse, et U est la limite de confiance la plus haute. Pour plus d'informations, consultez le livre blanc sur la méthode de Bonett, qui contient des simulations et d'autres renseignements.
Les limites de confiance pour le taux de variance s'obtiennent en mettant les limites de confiance du rapport des écarts types au carré.
Constante égalisatrice
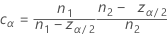
La constante disparaît lorsque les plans sont équilibrés et son effet devient négligeable lorsque les effectifs d'échantillons augmentent.
Erreur type de l'aplatissement regroupé
ErT(ρ) est l'erreur type de l'aplatissement regroupé, qui s'obtient comme suit :
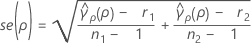
où ri = (ni - 3) / ni et 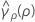 est l'aplatissement regroupé, qui s'obtient comme suit :
est l'aplatissement regroupé, qui s'obtient comme suit :
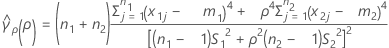
ErT(ρ) peut également être exprimé en termes de valeurs d'aplatissement de chaque échantillon. Pour plus d'informations, consultez la section consacrée au test pour la méthode de Bonett avec des plans équilibrés.
Notation
| Terme | Description |
|---|---|
| α | seuil de signification pour le test = 1 - (niveau de confiance / 100) |
| Si | écart type de l'échantillon i |
| ρ | rapport des écarts types de la population |
| zα/2 | point de percentile supérieur α/2 de la loi normale standard |
| ni | nombre d'observations dans l'échantillon i |
| Xij | je observation de l'échantillon i |
| mi | moyenne tronquée pour l'échantillon i avec des proportions de troncage de  |
Test pour la méthode de Levene
Formule
Le test de Levene est adapté pour les données continu. Il n'est pas disponible pour les données résumées.
Pour tester l'hypothèse nulle σ1 / σ2 = ρ avec le test de Levene, Minitab effectue une ANOVA unilatérale sur les valeurs Z1j et ρZ2j (où j = 1, …, n1 ou n2).
La statistique de test de Levene est égale à la valeur de la statistique F dans le tableau de résultats ANOVA. La valeur de p du test de Levene est égale à la valeur de p dans ce tableau ANOVA.
- H. Levene (1960), Contributions to Probability and Statistics, Stanford University Press, CA.
- M. B. Brown et A.B. Forsythe (1974), "Robust Tests for the Equality of Variance", Journal of the American Statistical Association, 69, 364–367.
Degrés de liberté
Selon l'hypothèse nulle, la statistique de test suit une distribution F avec les degrés de liberté DL1 et DL2.
DL1 = 1
DL2 = n1 + n2 – 2
Notation
| Terme | Description | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Zij | |Xi j – η i|
| ||||||||||
| σ1 | écart type de la première population | ||||||||||
| σ2 | écart type de la deuxième population | ||||||||||
| n 1 | effectif du premier échantillon | ||||||||||
| n 2 | effectif du deuxième échantillon |
Intervalles de confiance pour la méthode de Levene
Formule
Pour les données continues, Minitab calcule les limites de confiance pour le rapport (ρ) entre les écarts types de la population avec les formules suivantes. Pour obtenir les limites pour le rapport entre les variances de la population, mettez les valeurs ci-dessous au carré.
-
Si
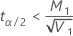 , limite inférieure =
, limite inférieure = 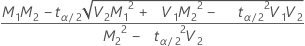
Si
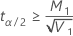 , aucune limite inférieure n'existe
, aucune limite inférieure n'existe -
Si
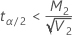 , limite supérieure =
, limite supérieure = 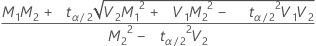
Si
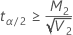 , aucune limite supérieure n'existe
, aucune limite supérieure n'existe
-
Si
 , alors
, alors 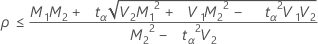
- Si
 , aucune limite supérieure n'existe
, aucune limite supérieure n'existe
-
Si
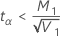 , alors
, alors 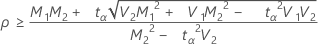
- Si
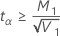 , aucune limite inférieure n'existe
, aucune limite inférieure n'existe
Notation
| Terme | Description |
|---|---|
| t α | la valeur critique α d'une distribution t avec n1 + n2 – 2 degrés de liberté |
| ηi | médiane de l'échantillon i |
| Zij |  où j = 1, 2, ... , ni et i = 1, 2, et Xij sont des observations individuelles où j = 1, 2, ... , ni et i = 1, 2, et Xij sont des observations individuelles |
| Mi | moyenne de Zij |
| Si2 | variance de l'échantillon de Zij |
| vi | 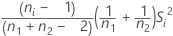 |
| ρ | σ1 / σ2 |
| n 1 | effectif du premier échantillon |
| n 2 | effectif du deuxième échantillon |
Test pour la méthode de test F
Le test F est adapté aux données normales. Pour tester l'hypothèse nulle σ1 / σ2 = ρ avec le test F, Minitab utilise les formules suivantes.
Formule pour la statistique de test
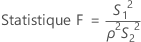
Formule pour les degrés de liberté
Selon l'hypothèse nulle, la statistique F suit une loi de distribution F avec les degrés de liberté DL1 et DL2.
DL1 = n1 – 1
DL2 = n2 – 1
Formule pour la valeur de p
- Pour un test unilatéral avec une hypothèse alternative de type "inférieur à", la valeur de p est égale à la probabilité d'obtenir une statistique F inférieure ou égale à la valeur observée d'après une distribution F avec des degrés de liberté DL1 et DL2.
- Pour un test bilatéral, où le rapport est inférieur à 1, la valeur de p est égale à deux fois la zone située sous la courbe F, inférieure à la valeur observée selon une distribution F avec des degrés de liberté DL1 et DL2.
- Pour un test bilatéral, où le rapport est supérieur à 1, la valeur de p est égale à deux fois la zone située sous la courbe F, supérieure à la valeur observée selon une distribution F avec des degrés de liberté DL1 et DL2.
- Pour un test unilatéral avec une hypothèse alternative de type "supérieur à", la valeur de p est égale à la probabilité d'obtenir une statistique F supérieure ou égale à la valeur observée d'après une distribution F avec des degrés de liberté DL1 et DL2.
Notation
| Terme | Description |
|---|---|
| ρ | σ1 / σ2 |
| σ1 | écart type de la première population |
| σ2 | écart type de la deuxième population |
| S21 | variance du premier échantillon |
| S22 | variance du deuxième échantillon |
| n 1 | effectif du premier échantillon |
| n 2 | effectif du deuxième échantillon |
Intervalles de confiance pour la méthode du test F
Lorsque les données suivent une distribution normale, Minitab calcule les bornes de confiance pour le rapport (ρ) entre les écarts types de la population avec les formules suivantes. Pour obtenir les bornes pour le rapport entre les variances de la population, mettez les valeurs ci-dessous au carré.
Formule
Lorsque vous indiquez une hypothèse alternative de type "non égal à", l'intervalle de confiance à 100(1 – α) % pour ρ s'obtient comme suit :

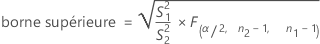
Lorsque vous indiquez une hypothèse alternative de type "inférieur à", la borne de confiance supérieure pour ρ, à un niveau de confiance de 100(1 – α) %, s'obtient comme suit :
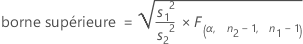
Lorsque vous indiquez une hypothèse alternative de type "supérieur à", la borne de confiance inférieure pour ρ, à un niveau de confiance de 100(1 – α) %, s'obtient comme suit :
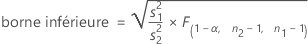
Notation
| Terme | Description |
|---|---|
| S1 | écart type du premier échantillon |
| S2 | écart type du deuxième échantillon |
| ρ | σ1 / σ2 |
| n 1 | effectif du premier échantillon |
| n 2 | effectif du deuxième échantillon |
| F(α/2, n2–1, n1–1) | α/2 valeur critique provenant de la distribution F avec degrés de liberté n2-1 et n1-1. |
