Sur ce thème
Hypothèse nulle et hypothèse alternative
- Hypothèse nulle
- L'hypothèse nulle affirme qu'un paramètre de la population (la moyenne, l'écart type, etc.) est égal à une valeur hypothétisée. L'hypothèse nulle est souvent une déclaration initiale basée sur des analyses précédentes ou des connaissances spécialisées.
- Hypothèse alternative
- L'hypothèse alternative affirme qu'un paramètre de la population est plus petit, plus grand ou différent de la valeur hypothétisée dans l'hypothèse nulle. L'hypothèse alternative est celle que vous pensez être vraie ou que vous espérez démontrer.
Interprétation
Dans les résultats, les hypothèses nulle et alternative vous permettent de vérifier que vous avez saisi une valeur correcte pour le rapport hypothétisé.
Seuil de signification
Le seuil de signification (noté alpha ou α) est le niveau maximal acceptable du risque de rejet de l'hypothèse nulle lorsqu'elle est vraie (erreur de type I). Généralement, vous choisissez le seuil de signification avant d'analyser les données. Dans Minitab, vous pouvez choisir le seuil de signification en indiquant le niveau de confiance, car le seuil de signification est égal à 1 moins le niveau de confiance. Le niveau de confiance par défaut étant 0,95 dans Minitab, le seuil de signification par défaut est 0,05.
Interprétation
Comparez le seuil de signification à la valeur de p pour décider s'il faut rejeter ou non l'hypothèse nulle (H0). Si la valeur de p est inférieure au seuil de signification, l'interprétation est généralement que les résultats sont statistiquement significatifs, et vous rejetez H0.
- Choisissez un seuil de signification plus important, tel que 0,10, pour être sûr de détecter toutes les différences qui puissent exister. Par exemple, un ingénieur qualité compare la stabilité de nouveaux roulements à billes à celle des roulements existants. Il doit s'assurer que les nouveaux roulements à billes sont absolument stables car, si ce n'est pas le cas, ils pourraient provoquer une catastrophe. L'ingénieur choisit un seuil de signification de 0,10 afin d'augmenter sa certitude de détecter toute différence possible dans la stabilité des roulements à billes.
- Choisissez un seuil de signification moins important, tel que 0,01, pour être sûr de détecter uniquement une différence existant réellement. Par exemple, un scientifique travaillant pour une entreprise pharmaceutique doit s'assurer de la véracité de l'affirmation selon laquelle le nouveau médicament de l'entreprise réduit significativement les symptômes. Il choisit un seuil de signification de 0,001 afin d'augmenter sa certitude qu'il existe une différence significative dans les symptômes.
N
L'effectif de l'échantillon (N) est le nombre d'observations total de l'échantillon.
Interprétation
L'effectif de l'échantillon a une influence sur l'intervalle de confiance et la puissance du test.
En général, plus l'échantillon est grand, plus l'intervalle de confiance est étroit. En outre, un effectif d'échantillon plus grand donne au test plus de puissance pour détecter une différence. Pour plus d'informations, reportez-vous à la rubrique Qu'est-ce que la puissance ?.
EcTyp
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données sur la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit.
L'écart type utilise les mêmes unités que les données.
Interprétation
L'écart type de chaque échantillon est une estimation de l'écart type de chaque population. Minitab utilise l'écart type pour estimer le rapport des écarts types de la population. Ce rapport est très important.
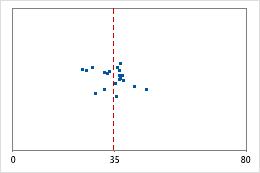
Hôpital 1
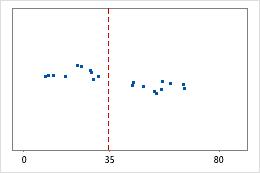
Hôpital 2
Durée jusqu'à la sortie de l'hôpital
Les administrateurs de deux hôpitaux étudient le temps que passent les patients dans le service des urgences de leurs établissements jusqu'à leur sortie. Bien que ces durées moyennes soient pratiquement identiques (35 minutes), les écarts types diffèrent de manière significative. L'écart type pour l'hôpital 1 est d'environ 6. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 6 minutes par rapport à la moyenne (ligne bleue). L'écart type pour l'hôpital 2 est d'environ 20. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 20 minutes par rapport à la moyenne (ligne bleue).
Variance
La variance mesure le degré de dispersion des données autour de leur moyenne. Elle est égale à l'écart type au carré.
Interprétation
La variance de chaque échantillon est une estimation de la variance de chaque population. Minitab utilise les variances afin d'estimer le rapport des variances de population. Ce rapport est très important.
Rapport des écarts types estimé
Le rapport des écarts types est l'écart type du premier échantillon divisé par celui du deuxième échantillon.
Interprétation
Le rapport estimé des écarts types des données de l'échantillon est une estimation du rapport des écarts types de population.
Le rapport estimé étant calculé à partir des données d'échantillon et non de l'ensemble de la population, il est peu probable que le rapport de l'échantillon soit égal à celui de la population. Pour mieux estimer le rapport, utilisez l'intervalle de confiance.
Rapport de variances estimé
Le rapport des variances est la variance du premier échantillon divisée par celle du deuxième échantillon.
Interprétation
Le rapport estimé des variances des données de l'échantillon est une estimation du rapport des variances de population.
Le rapport estimé étant calculé à partir des données d'échantillon et non de l'ensemble de la population, il est peu probable que le rapport de l'échantillon soit égal à celui de la population. Pour mieux estimer le rapport, utilisez l'intervalle de confiance.
Bornes et intervalle de confiance (IC)
L'intervalle de confiance fournit une étendue de valeurs probables pour le rapport de la population. Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Toutefois, si vous répétiez l'échantillonnage de nombreuses fois, un certain pourcentage des intervalles de confiance ou bornes obtenus contiendrait le rapport de population inconnu. Le pourcentage de ces intervalles de confiance ou bornes contenant le rapport est le niveau de confiance de l'intervalle. Par exemple, un niveau de confiance de 95 % indique que, sur 100 échantillons pris de façon aléatoire parmi la population, environ 95 de ces échantillons devraient produire des intervalles contenant le rapport de la population.
Une borne supérieure définit une valeur à laquelle le rapport de population est susceptible d'être inférieur. Une borne inférieure définit une valeur à laquelle le rapport de population est susceptible d'être supérieur.
L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon. Pour plus d'informations, reportez-vous à la rubrique Obtenir un intervalle de confiance plus précis.
Par défaut, le test à 2 variances affiche les résultats de la méthode de Levene et ceux de la méthode de Bonett. La méthode de Bonett est généralement plus fiable que celle de Levene. Toutefois, en cas de lois extrêmement asymétriques et à extrémités lourdes, la méthode de Levene est généralement plus fiable que celle de Bonett. N'utilisez le test F que si vous êtes certain que les données suivent une loi normale. Tout écart par rapport à la loi normale, même minime, peut avoir un impact important sur les résultats du test F. Pour plus d'informations, reportez-vous à la rubrique Dois-je utiliser la méthode de Bonett ou la méthode de Levene avec la fonction 2 variances ?.
Rapport des écarts types
| Rapport estimé | IC à 95% pour le rapport utilisant Bonett | IC à 95% pour le rapport utilisant Levene |
|---|---|---|
| 0,658241 | (0,372; 1,215) | (0,378; 1,296) |
Dans ces résultats, l'estimation du rapport des écarts types de la population pour les évaluations de deux hôpitaux est de 0,658. A l'aide de la méthode de Bonett, vous pouvez être sûr à 95 % que le rapport des écarts types de la population pour les évaluations des hôpitaux est compris entre 0,372 et 1,215.
DL
Les degrés de libertés (DL) représentent la quantité d'informations fournies par les données que vous pouvez "consommer" pour estimer les valeurs des paramètres de population inconnus et calculer la variabilité de ces estimations. Pour un test à 2 variances, les degrés de liberté se déterminent d'après le nombre d'observations de votre échantillon et dépendent également de la méthode utilisée par Minitab.
Interprétation
Minitab utilise les degrés de liberté pour déterminer la statistique du test. Les degrés de liberté sont déterminés par l'effectif de l'échantillon. L'accroissement de l'effectif de l'échantillon permet d'obtenir davantage d'informations sur la population, ce qui augmente les degrés de liberté.
Statistique de test pour la méthode de Bonett
La statistique de test est une statistique que Minitab calcule pour la méthode de Bonett en inversant les intervalles de confiance. La statistique de test de la méthode de Bonett n'est pas disponible pour les données résumées ou pour les données non équilibrées.
Interprétation
Vous pouvez comparer la statistique de test aux valeurs critiques de la loi du Khi deux pour déterminer s'il faut rejeter l'hypothèse nulle. Cependant, il est souvent plus pratique et plus commode d'utiliser la valeur de p du test pour cela. La valeur de p a la même moyenne quel que soit le test d'effectif, mais une même statistique de Khi deux peut indiquer des conclusions opposées en fonction de la taille de l'échantillon.
- Pour un test bilatéral, les valeurs critiques sont
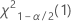et 
. Si la statistique de test est inférieure à la première valeur ou supérieure à la deuxième valeur, rejetez l'hypothèse nulle. Si la statistique de test se trouve entre la première et la deuxième valeur, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral avec une hypothèse alternative de type "inférieur à", la valeur critique est
. Si la statistique de test est inférieure à la valeur critique, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral d'une hypothèse de type "supérieur à", la valeur critique est de
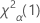. Si la statistique de test est supérieure à la valeur critique, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle.
La statistique de test sert à calculer la valeur de p.
Statistique de test pour la méthode de Levene
Le test utilise la statistique F ANOVA unilatérale appliquée à l'écart moyen absolu des observations. Par conséquent, l'application de la méthode de Levene est équivalente à l'application de la procédure ANOVA unilatérale à l'écart moyen absolu des observations. Pour des problèmes à 2 échantillons, cette méthode est également équivalente à l'application de la procédure t à 2 échantillons à l'écart moyen absolu des observations.
Interprétation
Vous pouvez comparer la statistique de test aux valeurs critiques de la loi F pour déterminer s'il faut rejeter l'hypothèse nulle. Cependant, il est souvent plus pratique et plus commode d'utiliser la valeur de p du test pour cela.
- Pour un test bilatéral, les valeurs critiques sont
et 
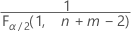. Si la statistique de test est inférieure à la première valeur ou supérieure à la deuxième valeur, rejetez l'hypothèse nulle. Si la statistique de test se trouve entre la première et la deuxième valeur, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral avec une hypothèse alternative de type "inférieur à", la valeur critique est
. Si la statistique de test est inférieure à la valeur critique, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral d'une hypothèse de type "supérieur à", la valeur critique est de
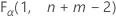. Si la statistique de test est supérieure à la valeur critique, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle.
La statistique de test sert à calculer la valeur de p.
Statistique de test pour la méthode F
La statistique de test est une statistique pour les tests Z qui mesure le rapport entre deux variances observées.
Interprétation
Vous pouvez comparer la statistique de test aux valeurs critiques de la loi F pour déterminer s'il faut rejeter l'hypothèse nulle. Cependant, il est souvent plus pratique et plus commode d'utiliser la valeur de p du test pour cela.
- Pour un test bilatéral, les valeurs critiques sont
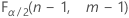et 
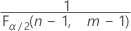. Si la statistique de test est inférieure à la première valeur ou supérieure à la deuxième valeur, rejetez l'hypothèse nulle. Si la statistique de test se trouve entre la première et la deuxième valeur, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral avec une hypothèse alternative de type "inférieur à", la valeur critique est
. Si la statistique de test est inférieure à la valeur critique, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral d'une hypothèse de type "supérieur à", la valeur critique est de
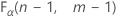. Si la statistique de test est supérieure à la valeur critique, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle.
La statistique de test sert à calculer la valeur de p.
valeur de p
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Une valeur de p inférieure fournit des preuves plus solides par rapport à l'hypothèse nulle.
Interprétation
Utilisez la valeur de p pour déterminer si la différence entre des variances ou des écarts types de population est statistiquement significative.
- Valeur de p ≤ α : le rapport des écarts types ou des variances est statistiquement significatif (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle. Vous pouvez conclure que le rapport des variances ou des écarts types de population n'est pas égal au rapport hypothétisé. Si vous n'avez pas spécifié de rapport hypothétisé, Minitab vérifie l'absence de différence entre les écarts types ou les variances (Rapport hypothétisé = 1). Utilisez vos connaissances afin de déterminer si la différence est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Signification statistique et pratique.
- Valeur de p > α : le rapport des écarts types ou des variances n'est pas statistiquement significatif (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que le rapport des variances ou des écarts types de population est statistiquement significatif. Vous devez vous assurer que votre test est assez puissant pour détecter une différence qui est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Puissance et effectif de l'échantillon pour 2 variances.
- Le test de Bonett est exact pour toute loi de distribution continue et ne requiert pas la normalité des données. Le test de Bonett est généralement plus fiable que celui de Levene.
- Le test de Levene est également exact pour toute loi de distribution continue. En cas de lois extrêmement asymétriques et à extrémités lourdes, la méthode de Levene est généralement plus fiable que celle de Bonett.
- Le test F n'est exact que pour des données normalement distribuées. Le moindre écart par rapport à la normalité peut entraîner un résultat imprécis pour le test F, y compris avec des échantillons importants. Toutefois, si les données sont conformes à la loi normale, le test F est généralement plus puissant que les méthodes de Bonett et de Levene.
Pour plus d'informations, reportez-vous à la rubrique Dois-je utiliser la méthode de Bonett ou la méthode de Levene avec la fonction 2 variances ?.
Graphique récapitulatif
Le diagramme récapitulatif indique les intervalles de confiance pour le rapport et pour les écarts types ou les variances de chaque échantillon. Le diagramme récapitulatif comporte également des boîtes à moustaches des données des échantillons et des valeurs de p pour les tests d'hypothèse.
Intervalles de confiance
L'intervalle de confiance fournit une étendue de valeurs probables pour le rapport de la population. Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Toutefois, si vous répétiez l'échantillonnage de nombreuses fois, un certain pourcentage des intervalles de confiance ou bornes obtenus contiendrait le rapport de population inconnu. Le pourcentage de ces intervalles de confiance ou bornes contenant le rapport est le niveau de confiance de l'intervalle. Par exemple, un niveau de confiance de 95 % indique que, sur 100 échantillons pris de façon aléatoire parmi la population, environ 95 de ces échantillons devraient produire des intervalles contenant le rapport de la population.
Une borne supérieure définit une valeur à laquelle le rapport de population est susceptible d'être inférieur. Une borne inférieure définit une valeur à laquelle le rapport de population est susceptible d'être supérieur.
Interprétation
L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon. Pour plus d'informations, reportez-vous à la rubrique Obtenir un intervalle de confiance plus précis.
Par défaut, le test à 2 variances affiche les résultats de la méthode de Levene et ceux de la méthode de Bonett. La méthode de Bonett est généralement plus fiable que celle de Levene. Toutefois, en cas de lois extrêmement asymétriques et à extrémités lourdes, la méthode de Levene est généralement plus fiable que celle de Bonett. N'utilisez le test F que si vous êtes certain que les données suivent une loi normale. Tout écart par rapport à la loi normale, même minime, peut avoir un impact important sur les résultats du test F. Pour plus d'informations, reportez-vous à la rubrique Dois-je utiliser la méthode de Bonett ou la méthode de Levene avec la fonction 2 variances ?.
Boîte à moustaches
Une boîte a moustaches fournit un récapitulatif graphique de la loi de distribution de chaque échantillon. Elle facilite la comparaison de la forme, de la tendance centrale et de la variabilité des échantillons.
Interprétation
Utilisez une boîte à moustaches pour examiner la dispersion des données et pour détecter d'éventuelles valeurs aberrantes. Les boîtes à moustaches sont plus adaptées lorsque l'effectif d'échantillon est supérieur à 20.
- Données asymétriques
-
Examinez de la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
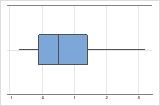
Asymétrie à droite
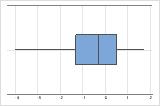
Asymétrie à gauche
La boîte à moustaches avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. La boîte à moustaches avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
Les données qui sont très asymétriques peuvent avoir une incidence sur la validité de la valeur de p si vos échantillons sont petits (l'un des échantillons contient moins de 20 valeurs). Si vos données sont très asymétriques et que vous avez un petit échantillon, pensez éventuellement à augmenter l'effectif d'échantillon.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
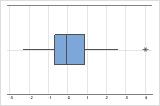
Sur une boîte à moustaches, les astérisques (*) indiquent les valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
Diagramme des valeurs individuelles
Un diagramme des valeurs individuelles présente les valeurs individuelles contenues dans chaque échantillon. Il facilite la comparaison des échantillons. Chaque cercle représente une observation. Un diagramme des valeurs individuelles est particulièrement utile lorsque vous disposez de relativement peu d'observations et que vous avez besoin d'évaluer l'effet de chacune d'entre elles.
Interprétation
Utilisez un diagramme des valeurs individuelles pour examiner la dispersion des données et pour détecter d'éventuelles valeurs aberrantes. Les diagrammes des valeurs individuelles sont plus adaptés lorsque l'effectif d'échantillon est inférieur à 50.
- Données asymétriques
-
Examinez de la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
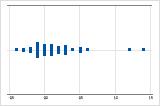
Asymétrie à droite
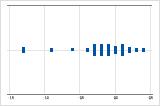
Asymétrie à gauche
Le diagramme des valeurs individuelles avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. Le diagramme des valeurs individuelles avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
Les données qui sont très asymétriques peuvent avoir une incidence sur la validité de la valeur de p si vos échantillons sont petits (l'un des échantillons contient moins de 20 valeurs). Si vos données sont très asymétriques et que vous avez un petit échantillon, pensez éventuellement à augmenter l'effectif d'échantillon.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
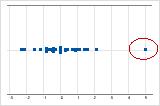
Sur un diagramme des valeurs individuelles, les valeurs de données anormalement élevées ou faibles indiquent de possibles valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
Histogramme
Un histogramme divise les valeurs des échantillons en plusieurs intervalles et représente l'effectif des valeurs contenues dans chaque intervalle par une barre.
Interprétation
Utilisez un histogramme pour évaluer la forme et la dispersion des données. Les histogrammes sont plus adaptés lorsque l'effectif d'échantillon est supérieur à 20.
- Données asymétriques
-
Examinez de la dispersion des données pour déterminer si elles semblent asymétriques. Lorsque les données sont asymétriques, la majorité d'entre elles sont situées sur le côté supérieur ou inférieur du graphique. En général, l'asymétrie est plus facile à détecter avec un histogramme ou une boîte à moustaches.
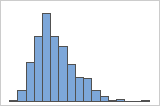
Asymétrie à droite
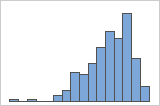
Asymétrie à gauche
L'histogramme avec des données asymétriques à droite illustre des temps d'attente. La plupart des temps d'attente sont relativement courts, seuls certains sont longs. L'histogramme avec des données asymétriques à gauche représente des données de temps de défaillance. Quelques éléments rencontrent une défaillance immédiatement, mais pour bien plus d'entre eux, elle survient plus tard.
Les données qui sont très asymétriques peuvent avoir une incidence sur la validité de la valeur de p si vos échantillons sont petits (l'un des échantillons contient moins de 20 valeurs). Si vos données sont très asymétriques et que vous avez un petit échantillon, pensez éventuellement à augmenter l'effectif d'échantillon.
- Valeurs aberrantes
-
Les valeurs aberrantes, qui sont des valeurs de données très éloignées des autres valeurs de données, peuvent avoir une incidence importante sur les résultats de votre analyse. En général, les valeurs aberrantes sont plus faciles à repérer sur une boîte à moustaches.
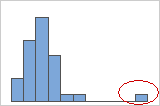
Sur un histogramme, des barres isolées à une extrémité ou l'autre du graphique indiquent de possibles valeurs aberrantes.
Essayez de déterminer la cause de toutes les valeurs aberrantes. Corrigez les erreurs de mesure ou d’entrée des données. Supprimez éventuellement les valeurs de données associées à des événements anormaux et uniques (aussi appelés causes spéciales). Ensuite, répétez l'analyse. Pour plus d'informations, reportez-vous à la rubrique Identification des valeurs aberrantes.
