Un consultant dans le domaine de la santé désire comparer le niveau de satisfaction des patients de deux hôpitaux. Le consultant collecte les évaluations effectuées par 20 patients pour chacun des hôpitaux.
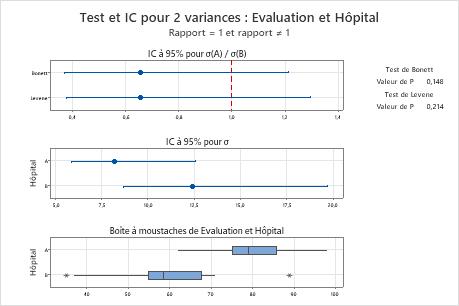
Le consultant effectue un test à 2 variances pour déterminer si les écarts types dans les notations des patients diffèrent selon l'hôpital.
- Ouvrez le fichier de données échantillons, ComparHôpitaux.MWX.
- Sélectionnez .
- Dans la liste déroulante, sélectionnez Les deux échantillons se trouvent dans une colonne.
- Dans la zone Echantillons, saisissez Evaluation.
- Dans la zone ID d'échantillons, saisissez Hôpital.
- Cliquez sur OK.
Interprétation des résultats
L'hypothèse nulle indique que le rapport entre les écarts types est de 1. Comme les valeurs de p sont supérieures au seuil de signification (indiqué par α ou alpha) de 0,05, le consultant ne peut pas rejeter l'hypothèse nulle. Le consultant n'est pas en mesure d'affirmer que les écarts types entre les hopitaux sont différents.
Méthode
| σ₁ : écart type de Evaluation lorsque Hôpital = A |
|---|
| σ₂ : écart type de Evaluation lorsque Hôpital = B |
| Rapport : σ₁/σ₂ |
| Les méthodes de Bonett et de Levene sont valides pour toute loi de distribution continue. |
Statistiques descriptives
| Hôpital | N | EcTyp | Variance | IC à 95% pour σ |
|---|---|---|---|---|
| A | 20 | 8,183 | 66,958 | (5,893; 12,597) |
| B | 20 | 12,431 | 154,537 | (8,693; 19,709) |
Rapport des écarts types
| Rapport estimé | IC à 95% pour le rapport utilisant Bonett | IC à 95% pour le rapport utilisant Levene |
|---|---|---|
| 0,658241 | (0,372; 1,215) | (0,378; 1,296) |
Test
| Hypothèse nulle | H₀ : σ₁ / σ₂ = 1 |
|---|---|
| Hypothèse alternative | H₁ : σ₁ / σ₂ ≠ 1 |
| Seuil de signification | α = 0,05 |
| Méthode | Statistique du test | DL1 | DL2 | Valeur de P |
|---|---|---|---|---|
| Bonett | 2,09 | 1 | 0,148 | |
| Levene | 1,60 | 1 | 38 | 0,214 |