Intervalle de confiance (IC)
Formule
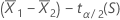et 
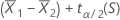
Notation
| Terme | Description |
|---|---|
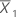 | moyenne du premier échantillon |
 | moyenne du deuxième échantillon |
| tα/2 | probabilité cumulée inverse de la loi de distribution t avec 1 – α/2 |
| α | 1 – niveau de confiance / 100 |
| s | écart type de l'échantillon calculé pour la statistique de test |
Valeur de t
Formule
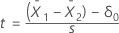
dépend de l'hypothèse de variance.
- Inégalité des variances
-
Lorsque vous émettez une hypothèse selon laquelle des variances sont inégales, l'écart type de l'échantillon de
est :
Les degrés de liberté sont :
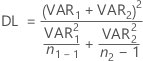
Si besoin, Minitab tronque les degrés de liberté à un entier, ce qui est une approche plus prudente que l'arrondissement.
- Egalité des variances
-
Lorsque vous supposez que des variances sont égales, la variance commune est estimée par la variance regroupée :
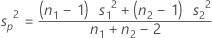L'écart type de
se calcule comme suit :
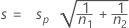
Les degrés de liberté de la statistique de test sont :
DL = n1 + n2 – 2
Notation
| Terme | Description |
|---|---|
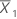 | moyenne du premier échantillon |
 | moyenne du deuxième échantillon |
| s | écart type d'échantillon de  |
| δ0 | différence hypothétisée entre les moyennes de deux populations |
| s1 | écart type du premier échantillon |
| s2 | écart type du deuxième échantillon |
| n 1 | effectif du premier échantillon |
| n 2 | effectif du deuxième échantillon |
| VAR1 |  |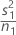
| VAR2 |  |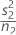
Calcul de l'écart type combiné
Supposons que la colonne C1 contienne la réponse et que la colonne C3 contienne la moyenne de chaque niveau de facteur. Par exemple :
| C1 | C2 | C3 |
|---|---|---|
| Réponse | Facteur | Moyenne |
| 18,95 | 1 | 14,5033 |
| 12,62 | 1 | 14,5033 |
| 11,94 | 1 | 14,5033 |
| 14,42 | 2 | 10,5567 |
| 10,06 | 2 | 10,5567 |
| 7,19 | 2 | 10,5567 |
- Sélectionnez .
- Dans la zone Stocker le résultat dans la variable, saisissez C4.
- Dans Expression, saisissez SQRT((SUM((C1 - C3)**2)) / (nombre total d'observations - nombre de groupes)) . Pour l'échantillon précédent, l'Expression pour l'écart type groupe serait : SQRT((SUM(('Réponse' - 'Moyenne')**2)) / (6 - 2))
La valeur enregistrée par Minitab est 3,75489.
Valeur de p
Formule
Le calcul de la valeur de p dépend de l'hypothèse alternative.
| Hypothèse alternative | Valeur de p |
|---|---|
 |
 |
 |
 |
 |
 |
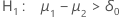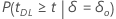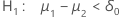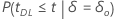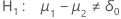- Inégalité des variances
-
Lorsque vous émettez une hypothèse selon laquelle des variances sont inégales, les degrés de liberté sont :
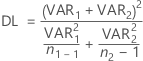
Si besoin, Minitab tronque les degrés de liberté à un entier, ce qui est une approche plus prudente que l'arrondissement.
- Egalité des variances
-
Lorsque vous émettez une hypothèse selon laquelle des variances sont égales, les degrés de liberté de la statistique de test sont :
DL = n1 + n2 – 2
Notation
| Terme | Description |
|---|---|
| μ1 | moyenne de la population du premier échantillon |
| μ1 | moyenne de la population du deuxième échantillon |
| n 1 | effectif du premier échantillon |
| n 2 | effectif du deuxième échantillon |
| δ0 | différence hypothétisée entre les moyennes de deux populations |
| t | statistique T des données échantillons |
| t | une variable aléatoire de la loi t avec DL degrés de liberté. |
| VAR1 |  |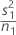
| VAR2 |  |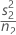
