Méthodes et formules pour la fonction Test de Poisson à 2 échantillons

Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Statistiques
Test d'hypothèse pour une différence de taux pour l'approximation de loi normale
Test d'hypothèse pour une différence de taux pour la méthode exacte
Test d'hypothèse pour une différence de taux avec la méthode des taux regroupés
Test d'hypothèse pour une différence de moyennes pour la méthode d'approximation de loi normale
Test hypothétique pour une différence de moyennes pour la méthode exacte
Test d'hypothèse pour une différence de moyennes pour la méthode des moyennes regroupées
Intervalle de confiance pour la différence de taux
Bornes de confiance pour la différence de taux
Intervalle de confiance pour la différence de moyennes
Bornes de confiance pour la différence de moyennes

Statistiques

Minitab génère les statistiques descriptives suivantes à partir de votre échantillon. Minitab affiche une moyenne seulement si vous modifiez la valeur par défaut de la "durée" pour définir 1.

Terme	Description
taux d'occurrence pour l'échantillon i

Terme	Description
nombre d'occurrences de la moyenne dans l'échantillon i

Test d'hypothèse pour une différence de taux pour l'approximation de loi normale

Formule

Le test d'approximation de loi normale est basé sur la statistique Z suivante, qui est répartie approximativement selon la loi normale standard, sous l'hypothèse nulle suivante :

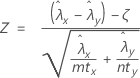
Minitab utilise les équations suivantes pour calculer les valeurs de p correspondant aux différentes hypothèses alternatives ci-dessous :

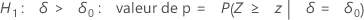
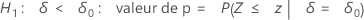
Notation

Terme	Description
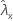	valeur observée pour le taux de l'échantillon X
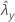	valeur observée pour le taux de l'échantillon Y
ζ	valeur réelle de la différence entre les taux de population de deux échantillons
ζ₀	valeur hypothétisée de la différence entre les taux de population de deux échantillons
m	effectif de l'échantillon X
n	effectif de l'échantillon Y
t_x	durée de l'échantillon X
t_y	durée de l'échantillon Y

Test d'hypothèse pour une différence de taux pour la méthode exacte

Formule

Lorsque la différence hypothétisée est égale à 0, Minitab teste l'hypothèse nulle suivante avec une procédure exacte :

H₀ : ζ = λ_x – λ_y = 0, ou H₀ : λ_x = λ_y

La procédure exacte est basée sur le fait suivant, en supposant que l'hypothèse nulle est vraie :

S | W ~ Binomiale (w, p)

où :

W = S + U

Minitab utilise les équations avec valeur de p suivantes pour les hypothèses alternatives respectives :

H₁ : ζ > 0 : valeur de p = P(S ≥ s | w = s + u, p = p₀)
H₁ : ζ < 0 : valeur de p = P(S ≤ s | w = s + u, p = p₀)
H₁ : ζ ≠ 0 :
- si P(S ≤ s | w = s + u, p = p₀) ≤ 0,5 ou P(S ≥ s | w = s + u, p = p₀) ≤ 0,5
  alors la valeur de p = 2 × min {P(S ≤ s | w = s + u, p = p₀), P(S ≥ s | w = s + u, p = p₀)}
- sinon, valeur de p = 1,0

où :

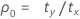
Notation

Terme	Description
	valeur observée pour le taux de l'échantillon X
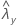	valeur observée pour le taux de l'échantillon Y
λ_x	valeur réelle du taux de la population X
λ_y	valeur réelle du taux de la population Y
ζ	valeur réelle de la différence entre les taux de population de deux échantillons
t_x	longueur de l'échantillon X
t_y	longueur de l'échantillon Y
m	effectif de l'échantillon X
n	effectif de l'échantillon Y

Test d'hypothèse pour une différence de taux avec la méthode des taux regroupés

Lorsque vous testez une différence de zéro avec l'hypothèse nulle ci-dessous, vous pouvez utiliser un taux regroupé pour les deux échantillons.

Formule

La procédure des taux regroupés est basée sur la statistique Z suivante, qui est répartie approximativement selon la loi normale standard, sous l'hypothèse nulle suivante :

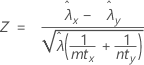
où :

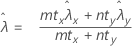
Minitab utilise les équations suivantes pour calculer les valeurs de p correspondant aux différentes hypothèses alternatives ci-dessous :

Notation

Terme	Description
	valeur observée pour le taux de l'échantillon X
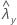	valeur observée pour le taux de l'échantillon Y
λ_x	valeur réelle du taux de la population X
λ_y	valeur réelle du taux de la population Y
ζ	valeur réelle de la différence entre les taux de population de deux échantillons
m	effectif de l'échantillon X
n	effectif de l'échantillon Y
t_x	durée de l'échantillon X
t_y	durée de l'échantillon Y

Test d'hypothèse pour une différence de moyennes pour la méthode d'approximation de loi normale

Formule

Le test d'approximation de loi normale est basé sur la statistique Z suivante, qui est répartie approximativement selon la loi normale standard, sous l'hypothèse nulle suivante :

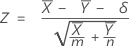
Minitab utilise les équations suivantes pour calculer les valeurs de p correspondant aux différentes hypothèses alternatives ci-dessous :

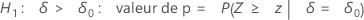
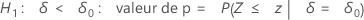
Notation

Terme	Description
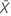	valeur observée pour le nombre moyen d'occurrences dans l'échantillon X
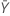	valeur observée pour le nombre moyen d'occurrences dans l'échantillon Y
δ	valeur réelle de la différence entre les moyennes de population de deux échantillons
δ ₀	valeur hypothétisée de la différence entre les moyennes de population de deux échantillons
m	effectif de l'échantillon X
n	effectif de l'échantillon Y

Test hypothétique pour une différence de moyennes pour la méthode exacte

Formule

Lorsque la différence hypothétisée est égale à 0, Minitab utilise une procédure exacte. La procédure exacte utilise l'hypothèse nulle suivante :

La procédure exacte est basée sur le fait suivant, en supposant que l'hypothèse nulle est vraie :

S | W ~ Binomiale (w, p)

où :

W = S + U

Minitab utilise les équations suivantes pour calculer les valeurs de p correspondant aux différentes hypothèses alternatives ci-dessous :

H₁ : δ > 0 : valeur de p = P(S ≥ s | w = s + u, δ = 0)

H₁ : δ < 0 : valeur de p = P(S ≤ s | w = s + u, δ = 0)

H₁ : δ ≠ 0 :

si P(S ≤ s|w = s + u, δ = 0) ≤ 0,5

ou P(S ≥ s|w = s + u, δ = 0) ≤ 0,5

alors :
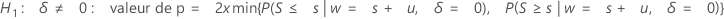
sinon, valeur de p = 1,0

Un test bilatéral n'est pas un test symétrique, sauf si m = n.

Notation

Terme	Description
μ_x	valeur réelle du nombre d'occurrences moyen dans la population X
μ_y	valeur réelle du nombre d'occurrences moyen dans la population Y
δ	valeur réelle de la différence entre les moyennes de population de deux échantillons
m	effectif de l'échantillon X
n	effectif de l'échantillon Y

Test d'hypothèse pour une différence de moyennes pour la méthode des moyennes regroupées

Formule

Lorsque vous testez une différence de zéro avec l'hypothèse nulle suivante, vous pouvez utiliser un taux regroupé pour les échantillons suivants :

La procédure des moyennes regroupées est basée sur la valeur Z suivante, qui est répartie approximativement selon la loi normale standard, sous l'hypothèse nulle suivante :

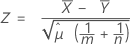
où :

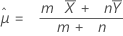
Minitab utilise les équations avec valeur p suivantes pour les hypothèses alternatives respectives :

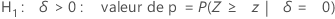
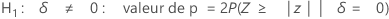
Notation

Terme	Description
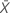	valeur observée pour le nombre moyen d'occurrences dans l'échantillon X
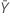	valeur observée pour le nombre moyen d'occurrences dans l'échantillon Y
µ_x	valeur réelle du nombre d'occurrences moyen dans la population X
µ_y	valeur réelle du nombre d'occurrences moyen dans la population Y
δ	valeur réelle de la différence entre les moyennes de population de deux échantillons
m	effectif de l'échantillon X
n	effectif de l'échantillon Y

Intervalle de confiance pour la différence de taux

Formule

Un intervalle de confiance à 100(1 – α) % pour la différence entre deux taux de Poisson de populations s'obtient comme suit :

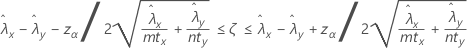
Notation

Terme	Description
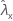	valeur observée pour le taux de l'échantillon X
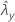	valeur observée pour le taux de l'échantillon Y
ζ	valeur réelle de la différence entre les taux de population de deux échantillons
z_x	point de percentile supérieur x de la loi normale standard, où 0 < x < 1
m	effectif de l'échantillon X
n	effectif de l'échantillon Y
t_x	durée de l'échantillon X
t_y	durée de l'échantillon Y

Bornes de confiance pour la différence de taux

Formule

Lorsque vous indiquez un test de type "supérieur à", la borne de confiance inférieure pour la différence entre deux taux de Poisson de populations, à un niveau de confiance de 100(1 – α) %, s'obtient comme suit :

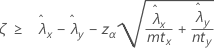
Lorsque vous indiquez un test de type "inférieur à", la borne de confiance supérieure pour la différence entre deux taux de Poisson de populations, à un niveau de confiance de 100(1 – α) %, s'obtient comme suit :

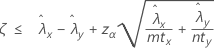
Notation

Terme	Description
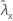	valeur observée pour le taux de l'échantillon X
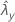	valeur observée pour le taux de l'échantillon Y
ζ	valeur réelle de la différence entre les taux de population de deux échantillons
z_x	le point percentile supérieur x de la loi normale standard, où 0 < x < 1
m	effectif de l'échantillon X
n	Effectif de l'échantillon Y
t_x	longueur de l'échantillon X
t_y	longueur de l'échantillon Y

Intervalle de confiance pour la différence de moyennes

Formule

Un intervalle de confiance à 100(1 – α) % pour la différence entre deux moyennes de Poisson de populations s'obtient comme suit :

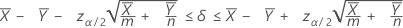
Notation

Terme	Description
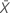	valeur observée pour le nombre moyen d'occurrences dans l'échantillon X
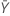	valeur observée pour le nombre moyen d'occurrences dans l'échantillon Y
δ	valeur réelle de la différence entre les moyennes de population de deux échantillons
z_x	point de percentile supérieur x de la loi normale standard, où 0 < x < 1
m	effectif de l'échantillon X
n	effectif de l'échantillon Y

Bornes de confiance pour la différence de moyennes

Formule

Lorsque vous indiquez un test de type "supérieur à", la borne de confiance inférieure pour la différence entre deux moyennes de Poisson de populations, à un niveau de confiance de 100(1 – α) %, s'obtient comme suit :

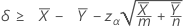
Lorsque vous indiquez un test de type "inférieur à", la borne de confiance supérieure pour la différence entre deux moyennes de Poisson de populations, à un niveau de confiance de 100(1 – α) %, s'obtient comme suit :

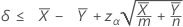
Notation

Terme	Description
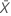	valeur observée pour le nombre moyen d'occurrences dans l'échantillon X
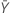	valeur observée pour le nombre moyen d'occurrences dans l'échantillon Y
δ	valeur réelle de la différence entre les moyennes de population de deux échantillons
z_x	point de percentile supérieur x de la loi normale standard, où 0 < x < 1
m	effectif de l'échantillon X
n	effectif de l'échantillon Y