Sélectionnez la méthode ou la formule de votre choix.
Intervalle de confiance (IC)
Formule
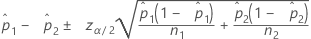
Notation
| Terme | Description |
|---|---|
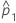 | estimation de la première proportion de la population |
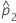 | estimation de la deuxième proportion de la population |
| n1 | nombre d'essais dans le premier échantillon |
| n2 | nombre d'essais dans le deuxième échantillon |
| zα/2 | probabilité cumulée inverse de la loi de distribution normale standard avec 1 – α/2 |
| α | 1 – niveau de confiance / 100 |
Test d'approximation normale
Le calcul de la statistique de test Z dépend de la méthode utilisée pour estimer p.
- Estimations individuelles de p
- Par défaut, Minitab utilise des estimations individuelles de p pour chaque population et calcule Z comme suit :
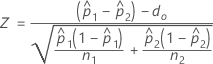
- Estimation regroupée de p
- Si la différence du test hypothétisé est de zéro et que vous choisissez d'utiliser une estimation groupée de p pour le test, Minitab calcule Z comme suit :
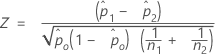
La valeur de p pour chaque hypothèse alternative est :
- H1 : p1 > p2 : valeur de p = P(Z1 ≥ z)
- H1 : p1 < p2 : vaeur de p = P(Z1 ≤ z)
- H1 : p1 ≠ p2 : valeur de p = 2P(Z1 ≥ z)
Calculez ces probabilités selon la loi normale standard.
Notation
| Terme | Description |
|---|---|
| p1 | proportion réelle d'événements dans la première population |
| p2 | proportion réelle d'événements dans la deuxième population |
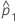 | proportion d'événements observée dans le premier échantillon |
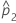 | proportion d'événements observée dans le deuxième échantillon |
| n1 | nombre d'essais dans le premier échantillon |
| n2 | nombre d'essais dans le deuxième échantillon |
| d0 | différence hypothétisée entre les première et deuxième proportions |
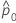 | 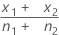 |
| x1 | nombre d'événements dans le premier échantillon |
| x2 | nombre d'événements dans le deuxième échantillon |
Test exact de Fisher
Minitab effectue le test exact de Fisher, en plus d'un test basé sur une approximation normale. Le test exact de Fisher est valide pour tous les effectifs d'échantillons.
Formule
Dans l'hypothèse nulle, le nombre d'événements dans le premier échantillon (x1) a une distribution hypergéométrique avec les paramètres suivants :
- Effectif de la population = n1 + n2
- Nombre d'événements dans la population = x1 + x2
- Effectif de l'échantillon = n1
Soit f( ) et F( ) la PDF et la CDF de cette dstribution hypergéométrique, respectivement. La valeur Mode désigne le mode. Les valeurs de p pour chaque hypothèse alternative sont les suivantes :
- H1 : p1 < p2
valeur de p = F(x1)
- H1 : p1 > p2
valeur de p = 1 – F(x1 – 1)
- H1 : p1 ≠ p2
Trois cas existent :
- Cas 1 : x1 < Mode
valeur de p = p inférieur + p supérieur
Terme Description p inférieur F(x1) p supérieur 1 – F(y – 1) y plus petit entier > Mode tel que f(y) <f(x1) Remarque
p supérieur peut être égal à zéro.
- Cas 2 : x1 = Mode
valeur de p = 1,0
- Cas 3 : x1 > Mode
valeur de p = p inférieur + p supérieur
Terme Description p supérieur 1 – F(x1 – 1) p inférieur F(y) y plus gros entier < Mode tel que f(y) < f(x1) Remarque
p inférieur peut être égal à zéro.
- Cas 1 : x1 < Mode
Notation
| Terme | Description |
|---|---|
| p1 | proportion réelle d'événements dans la première population |
| p2 | proportion réelle d'événements dans la deuxième population |
| x1 | nombre d'événements dans le premier échantillon |
| x2 | nombre d'événements dans le deuxième échantillon |
| n1 | nombre d'essais dans le premier échantillon |
| n2 | nombre d'essais dans le deuxième échantillon |
