Sur ce thème
Hypothèse nulle et hypothèse alternative
- Hypothèse nulle
- L'hypothèse nulle affirme qu'un paramètre de la population (la moyenne, l'écart type, etc.) est égal à une valeur hypothétisée. L'hypothèse nulle est souvent une déclaration initiale basée sur des analyses précédentes ou des connaissances spécialisées.
- Hypothèse alternative
- L'hypothèse alternative affirme qu'un paramètre de la population est plus petit, plus grand ou différent de la valeur hypothétisée dans l'hypothèse nulle. L'hypothèse alternative est celle que vous pensez être vraie ou que vous espérez démontrer.
Interprétation
Dans les résultats, les hypothèses nulle et alternative vous permettent de vérifier que vous avez saisi une valeur correcte pour la variance ou l'écart type hypothétisé.
N
L'effectif de l'échantillon (N) est le nombre d'observations total de l'échantillon.
Interprétation
L'effectif de l'échantillon a une influence sur l'intervalle de confiance et la puissance du test.
En général, plus l'échantillon est grand, plus l'intervalle de confiance est étroit. En outre, un effectif d'échantillon plus grand donne au test plus de puissance pour détecter une différence. Pour plus d'informations, reportez-vous à la rubrique Qu'est-ce que la puissance ?.
EcTyp
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données sur la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit.
L'écart type utilise les mêmes unités que les données.
Interprétation
L'écart type des données échantillons est une estimation de l'écart type de la population.
L'écart type étant calculé à partir des données d'échantillon et non de l'ensemble de la population, il est peu probable que l'écart type de l'échantillon soit égal à celui de la population. Pour mieux estimer l'écart type de la population, utilisez l'intervalle de confiance.
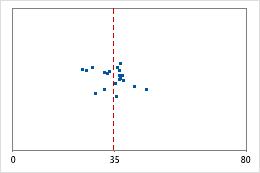
Hôpital 1
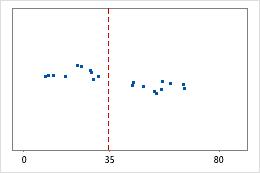
Hôpital 2
Durée jusqu'à la sortie de l'hôpital
Les administrateurs de deux hôpitaux étudient le temps que passent les patients dans le service des urgences de leurs établissements jusqu'à leur sortie. Bien que ces durées moyennes soient pratiquement identiques (35 minutes), les écarts types diffèrent de manière significative. L'écart type pour l'hôpital 1 est d'environ 6. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 6 minutes par rapport à la moyenne (ligne bleue). L'écart type pour l'hôpital 2 est d'environ 20. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 20 minutes par rapport à la moyenne (ligne bleue).
Variance
La variance mesure le degré de dispersion des données autour de leur moyenne. Elle est égale à l'écart type au carré.
Interprétation
La variance des données de l'échantillon est une estimation de la variance de la population.
La variance étant calculée à partir des données d'échantillon et non de l'ensemble de la population, il est peu probable que la variance de l'échantillon soit égale à celle de la population. Pour mieux estimer la variance de la population, utilisez l'intervalle de confiance.
Bornes et intervalle de confiance (IC)
L'intervalle de confiance fournit une étendue des valeurs probables pour l'écart type et la variance de la population. Les échantillons étant aléatoires, il est peu probable que deux échantillons d'une population donnent des intervalles de confiance identiques. Toutefois, si vous répétiez l'échantillonnage de nombreuses fois, un certain pourcentage des intervalles de confiance ou bornes obtenus contiendrait l'écart type et la variance de population inconnus. Le pourcentage de ces intervalles de confiance ou bornes contenant l'écart type ou la variance est le niveau de confiance de l'intervalle. Par exemple, un niveau de confiance de 95 % indique que, sur 100 échantillons pris de façon aléatoire parmi la population, environ 95 de ces échantillons devraient produire des intervalles contenant l'écart type ou la variance de la population.
Une borne supérieure définit une valeur à laquelle l'écart type ou la variance de la population sont susceptibles d'être inférieurs. Une borne inférieure définit une valeur à laquelle l'écart type ou la variance de la population sont susceptibles d'être supérieurs.
L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon. Pour plus d'informations, reportez-vous à la rubrique Obtenir un intervalle de confiance plus précis.
Remarque
Lorsque vous indiquez une colonne de données, Minitab calcule uniquement un intervalle de confiance pour l'écart type.
Remarque
Minitab ne peut pas calculer la méthode de Bonett avec des données résumées.
Statistiques descriptives
| N | EcTyp | Variance | IC à 95% pour σ utilisant Bonett | IC à 95% pour σ utilisant Khi deux |
|---|---|---|---|---|
| 50 | 0,871 | 0,759 | (0,704; 1,121) | (0,728; 1,085) |
Dans ces résultats, l'estimation de l'écart type standard de la population pour la longueur de rayons lumineux est de 0,871 et l'estimation de la variance de la population est de 0,759. Etant donné que les données n'ont pas réussi le test de normalité, utilisez la méthode de Bonett. Vous pouvez être sûr à 95 % que l'écart type de la population est compris entre 0,704 et 1,121.
Statistique de test
La statistique de test est une statistique pour les tests de Khi deux qui mesure le rapport entre une variance observée et sa variance hypothétisée.
Interprétation
Vous pouvez comparer la statistique de test aux valeurs critiques de la loi du Khi deux pour déterminer s'il faut rejeter l'hypothèse nulle. Cependant, il est souvent plus pratique et plus commode d'utiliser la valeur de p du test pour cela. La valeur de p a la même moyenne quel que soit le test d'effectif, mais une même statistique de Khi deux peut indiquer des conclusions opposées en fonction de la taille de l'échantillon.
- Pour un test bilatéral, les valeurs critiques sont
et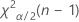 
. Si la statistique de test est inférieure à la première valeur ou supérieure à la deuxième valeur, rejetez l'hypothèse nulle. Si elle se trouve entre les deux, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral avec une hypothèse alternative de type "inférieur à", la valeur critique est
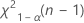. Si la statistique de test est inférieure à la valeur, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle. - Pour un test unilatéral d'une hypothèse de type "supérieur à", la valeur critique est de
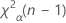. Si la statistique de test est supérieure à la valeur, rejetez l'hypothèse nulle. Dans le cas contraire, vous ne pouvez pas rejeter l'hypothèse nulle.
La statistique de test sert à calculer la valeur de p. Comme il n'existe pas de statistique de test pour la méthode Bonnet, Minitab utilise les régions de rejet définies par les limites de confiance pour calculer une valeur de p.
DL
Les degrés de libertés (DL) représentent la quantité d'informations disponibles dans les données pour estimer les valeurs des paramètres inconnus et calculer la variabilité de ces estimations. Pour un test à 1 variance, les degrés de liberté se déterminent d'après le nombre d'observations de votre échantillon.
Interprétation
Minitab utilise les degrés de liberté pour déterminer la statistique du test. Les degrés de liberté sont déterminés par l'effectif de l'échantillon. L'accroissement de l'effectif de l'échantillon permet d'obtenir davantage d'informations sur la population, ce qui augmente les degrés de liberté.
valeur de p
La valeur de p est la probabilité qui mesure le degré de certitude avec lequel il est possible d'invalider l'hypothèse nulle. Une valeur de p inférieure fournit des preuves plus solides par rapport à l'hypothèse nulle.
Interprétation
Utilisez la valeur de p pour déterminer si la variance ou l'écart type de la population est statistiquement différent de la variance ou l'écart type hypothétisé.
- Valeur de p ≤ α : la différence entre les variances ou les écarts types est statistiquement significative (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle. Vous pouvez conclure que la différence entre la variance ou l'écart type de la population et les valeurs hypothétisées est statistiquement significative. Utilisez vos connaissances afin de déterminer si la différence est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Signification statistique et pratique.
- Valeur de p > α : la différence entre les variances ou les écarts types n'est pas statistiquement significative (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que la différence entre l'écart type ou la variance de la population et les valeurs hypothétisées est statistiquement significative. Vous devez vous assurer que votre test est assez puissant pour détecter une différence qui est significative dans la pratique. Pour plus d'informations, reportez-vous à la rubrique Puissance et effectif de l'échantillon pour 1 variance.
Remarque
Lorsque vous disposez de données résumées, Minitab ne peut pas calculer une valeur de p pour la méthode de Bonett.
