Sur ce thème
Statistiques
| Terme | Description |
|---|---|
| taux d'occurrence |
 |
| occurrence moyenne |
 |
Le taux est égal au nombre moyen d'occurrences par longueur d'unité d'observation. La moyenne est le nombre moyen d'occurrences dans tout l'échantillon. Si la longueur est égale à 1, le taux et la moyenne sont égaux.
Valeur de p pour le test exact
Formule
- H1 : λ > λ0 : valeur de p = P(S ≥ s | λ = λ0) où S a une loi de Poisson avec une moyenne de nλ0t.
- H1 : λ < λ0 : valeur de p = P(S ≤ s | λ = λ0) où S a une loi de Poisson avec une moyenne de nλ0t.
- H1 : λ ≠ λ0 : Minitab utilise un test de rapport de vraisemblance, comme suit :
Définissez la fonction G(s), qui exprime le test de rapport de probabilité en termes de s, le nombre total d'occurrences dans le procédé Poisson :

- si 0 ≤ s < nλ0t, résolvez l'équation G(y) = G(s) pour y dans l'intervalle (nλ0t, enλ0t] ;
valeur de p = P(S ≤ s | λ = λ0) + P(S ≥ y | λ = λ0)
- si s = nλ0t, alors
valeur de p = 1,00
- si nλ0t < s ≤ enλ0t, résolvez l'équation G(y) = G(s) pour y dans l'intervalle [0, nλ0t) ;
valeur de p = P(S ≤ y | λ = λ0) + P(S ≥ s | λ = λ0)
- si s > enλ0t, le test est unilatéral, et
valeur de p = P(S ≥ s | λ = λ0)
où S a une loi de Poisson avec une moyenne de nλ0t.
- si 0 ≤ s < nλ0t, résolvez l'équation G(y) = G(s) pour y dans l'intervalle (nλ0t, enλ0t] ;
Notation
| Terme | Description |
|---|---|
| s | nombre total d'occurrences dans le procédé de Poisson |
| t | "durée" de l'observation |
| λ0 | valeur hypothétisée du paramètre du taux de la population |
| λ | valeur réelle du paramètre du taux de la population |
| n | effectif d'échantillon |
| e | 2,71828, environ |
Intervalles et bornes de confiance pour le test exact
Intervalles de confiance
Un intervalle de confiance exact à 100(1 – α) %, pour le taux d'occurrence d'un procédé de Poisson s'obtient comme suit :
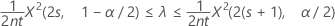
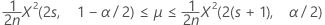
Bornes de confiance
Lorsque vous indiquez un test unilatéral, Minitab calcule une borne de confiance unilatérale à 100(1 – α) %, selon la direction de l'hypothèse alternative.
-
Si vous indiquez une hypothèse alternative de type "supérieur à", la borne inférieure exacte à 100(1 – α) % du taux s'obtient comme suit :
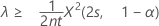
La borne inférieure exacte à 100(1-α) % de la moyenne s'obtient comme suit :
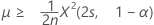
-
Si vous indiquez une hypothèse alternative de type "inférieur à", la borne supérieure exacte à 100(1 – α) % du taux s'obtient comme suit :
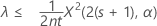
La borne supérieure exacte à 100(1 - α) % de la moyenne s'obtient comme suit :
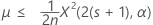
Notation
| Terme | Description |
|---|---|
| s | nombre total d'occurrences dans le procédé de Poisson |
| t | "durée" de l'observation |
| λ | valeur réelle du taux de la population |
| μ | valeur réelle de la moyenne de la population |
| Χ2(p, x) | percentile supérieur x de la loi de distribution X2 avec p degrés de liberté, où 0 < x < 1. |
| α | niveau alpha de l'intervalle de confiance à 100(1 –α) % |
| n | effectif d'échantillon |
Valeur de p pour l'approximation selon la loi normale
Les approximations selon la loi normale sont valides si le nombre total d'occurrences est supérieur à 10.
Formule
Le test d'hypothèse basé sur l'approximation selon la loi normale de la fonction Test de Poisson à 1 échantillon utilise les équations suivantes pour calculer les valeurs de p associées aux hypothèses alternatives indiquées :
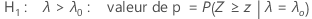
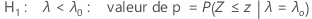
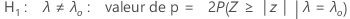
Notation
| Terme | Description |
|---|---|
| Z | 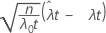 |
| t | "durée" de l'observation |
| λ 0 | valeur hypothétisée du paramètre du taux de la population |
| λ | valeur réelle du paramètre du taux de la population |
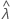 | valeur observée de la statistique du taux de l'échantillon |
| n | effectif d'échantillon |
Intervalles et bornes de confiance pour l'approximation selon la loi normale
Intervalles de confiance
Un intervalle de confiance à 100(1 – α) %, basé sur une approximation selon la loi normale, pour le taux d'occurrence d'un procédé de Poisson, s'obtient comme suit :
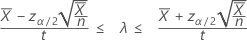
Lorsque vous indiquez une valeur pour la "durée", Minitab affiche également un intervalle de confiance pour le nombre moyen d'occurrences. Cet intervalle de confiance s'obtient comme suit :
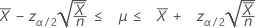
Bornes de confiance
Lorsque vous indiquez un test unilatéral, Minitab calcule une borne de confiance unilatérale à 100(1 – α) %, selon la direction de l'hypothèse alternative.-
Si vous indiquez une hypothèse alternative de type "supérieur à", la borne inférieure exacte à 100(1 – α) % du taux s'obtient comme suit :
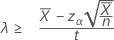
Si vous indiquez une valeur pour la "durée", la borne inférieure exacte à 100(1-α) % de la moyenne s'obtient comme suit :
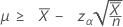
-
Si vous indiquez une hypothèse alternative de type "inférieur à", la borne supérieure exacte à 100(1 – α) % du taux s'obtient comme suit :
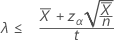
Si vous indiquez une valeur pour la "durée", la borne supérieure exacte de 100(1 - α) % de la moyenne s'obtient comme suit :
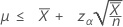
Notation
| Terme | Description |
|---|---|
| s | nombre total d'occurrences dans le procédé de Poisson |
| t | "durée" de l'observation |
| λ | valeur réelle du taux de la population |
| μ | valeur réelle de la moyenne de la population |
| Zx | point de percentile supérieur x de la loi normale standard, où 0 < x < 1. |
| α | niveau alpha de l'intervalle de confiance à 100(1 –α) % |
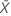 | nombre d'occurrences moyen dans l'échantillon |
| n | effectif d'échantillon |
