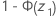Sur ce thème
- Ajustement de l’intervalle de confiance exact de Blaker et des méthodes de test
- Méthode de l’intervalle de confiance exact de Clopper-Pearson
- Test correspondant à l’intervalle de confiance exact de Clopper-Pearson
- Méthode de l’intervalle de confiance du score de Wilson
- Test de score
- Intervalle de confiance et méthodes d’essai d’Agresti-Coull
- Intervalle de confiance pour l’approximation de la normale de Wald (application Web)
Ajustement de l’intervalle de confiance exact de Blaker et des méthodes de test
La méthode exacte de Blaker ajustée produit des intervalles de confiance bilatéraux pour la proportion d’événements et produit des valeurs de p pour l’hypothèse alternative de p ≠ p0. Blaker12 fournit un intervalle de confiance exact et bilatéral en inversant la fonction de valeur p d’un test exact. Les intervalles de Clopper-Pearson sont plus larges et contiennent toujours les intervalles de confiance de Blaker. Les intervalles de la méthode exacte de Blaker sont imbriqués. Cette propriété signifie que les intervalles de confiance avec des niveaux de confiance plus élevés contiennent des intervalles de confiance avec des niveaux de confiance plus faibles. Par exemple, un intervalle de confiance à 95 % de Blaker exact et bilatéral contient l’intervalle de confiance à 90 % correspondant.
La méthode exacte originale de Blaker a 2 limitations. L’une des limites est que l’algorithme numérique pour calculer les intervalles de confiance est lent, en particulier lorsque la taille de l’échantillon est grande. Une autre limite est que, pour certaines données, la méthode exacte originale de Blaker produit un intervalle qui couvre une proportion hypothétique lorsque la valeur de p est inférieure au niveau de signification qui correspond au niveau de confiance. La limitation survient également lorsque l’intervalle de confiance ne contient pas de proportion hypothétique lorsque la valeur de p est supérieure au niveau de signification qui correspond au niveau de confiance.
Pour surmonter ces limitations, l’analyse dans Minitab Statistical Software produit l’intervalle de confiance et la valeur de p à l’aide de l’algorithme de Klaschka et Reiczigel.3 Le nom de cette méthode est la méthode exacte de Blaker ajustée. Cet algorithme numérique est plus rapide à calculer et produit des intervalles de confiance et des tests qui concordent en général. Les intervalles de confiance de Blaker ajustés sont également exacts et imbriqués.
Pour une hypothèse alternative avec inférieur ou supérieur à, l’analyse utilise la méthode exacte de Clopper-Pearson.
Méthode de l’intervalle de confiance exact de Clopper-Pearson
L’intervalle (PL, PU) est un intervalle de confiance bilatéral de 100(1 – α)% de p. Lorsque l’échantillon ne comporte aucun événement, la limite inférieure est 0. Lorsque l’échantillon ne contient que des événements, la limite supérieure est 1.
Limite inférieure
Formule

Notation
| Terme | Description |
|---|---|
| v1 | 2x |
| v2 | 2(n – x + 1) |
| x | nombre d'événements |
| n | Nombre de répliques |
| F | point inférieur α/2 de la loi F avec v1 et v2 degrés de liberté |
Limite supérieure
Formule

Notation
| Terme | Description |
|---|---|
| v1 | 2(x + 1) |
| v2 | 2(n – x) |
| x | nombre d'événements |
| n | Nombre de répliques |
| F | point supérieur α/2 de la loi F avec v1 et v2 degrés de liberté |
Test correspondant à l’intervalle de confiance exact de Clopper-Pearson
Formule
- Ha: p ≠ p0
- valeur de p =
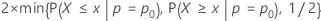
- Ha: p > p0
- valeur_p = P{ X ≥ x | p = po}
- Ha: p < p0
- valeur_p = P{ X ≤ x | p = po}
Notation
| Terme | Description |
|---|---|
| p0 | proportion hypothétisée |
| n | Nombre de répliques |
| p | probabilité d'un événement |
| x | nombre d'événements |
Méthode de l’intervalle de confiance du score de Wilson
Wilson4 inverse le test de score pour obtenir des intervalles de confiance que Minitab Statistical Software nomme intervalles de confiance Wilson-score. Les intervalles de score de Wilson ont deux formes, l’une sans correction de continuité et l’autre avec une correction de continuité. La couverture des intervalles sans correction est parfois inférieure au niveau de confiance nominal. Le niveau de confiance réel des intervalles avec la correction est au moins le niveau de confiance nominal. Pour les deux méthodes, lorsque l’échantillon n’a pas d’événements, la limite inférieure est 0. Lorsque l’échantillon ne contient que des événements, la limite supérieure est 1.
Intervalles sans correction de continuité
L’intervalle de confiance bilatéral de 100(1 – α)% a la formule suivante :
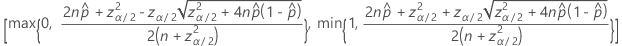
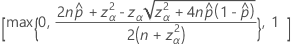
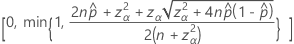
Intervalles avec la correction de continuité
La borne inférieure de l’intervalle bilatéral 100(1 – α)% a la formule suivante :
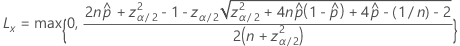
La limite supérieure de l’intervalle bilatéral de 100(1 – α)% a la formule suivante :
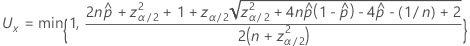
La limite inférieure unilatérale de 100(1 – α)% a la formule suivante :
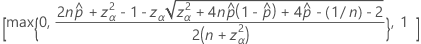
La limite supérieure unilatérale de 100(1 – α)% a la formule suivante :
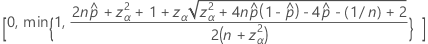
Notation
| Terme | Description |
|---|---|
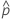 | probabilité observée, 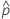 = x / n = x / n |
| x | nombre d'événements |
| n | Nombre de répliques |
| zγ | le centile supérieur de la loi normale standard à γ |
| α | 1 – niveau de confiance / 100 |
Test de score
Méthode sans correction de continuité
Le test qui correspond à l’intervalle de confiance du score de Wilson et à la méthode d’approximation normale (application Web) est le test de score bien connu. La statistique du test de score a l’équation suivante :
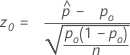
- Ha: p ≠ p0
- valeur de p =
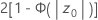
- Ha: p > p0
- valeur de p =

- Ha: p < p0
- valeur de p =

Méthode avec correction de continuité
La statistique de test et la valeur de p pour la procédure avec une correction de continuité dépendent de l’hypothèse alternative.
- Ha: p ≠ p0
-
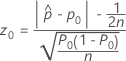
- Ha: p > p0
-
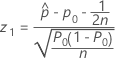
- Ha: p < p0
-
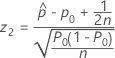
Notation
| Terme | Description |
|---|---|
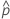 | probabilité observée, x/n |
| x | nombre d'événements |
| n | Nombre de répliques |
| p0 | proportion hypothétisée |
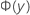 | Fonction de distribution cumulative de la loi normale standard en y |
Intervalle de confiance et méthodes d’essai d’Agresti-Coull
Intervalle de confiance
Agresti et Coull5 fournissent un ajustement à la méthode de Wald pour les intervalles de confiance qui améliore les propriétés de couverture. Pour un intervalle de confiance bilatéral à 95 %, l’ajustement additionne approximativement 2 événements et 2 non-événements, puis calcule les intervalles de confiance à partir des formules des formules de l’intervalle de confiance de Wald. Lorsque l’échantillon ne comporte aucun événement, la limite inférieure est 0. Lorsque l’échantillon ne contient que des événements, la limite supérieure est 1.
L’intervalle bilatéral de 100(1 – α)% a la formule suivante :
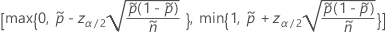
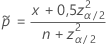
et
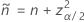
La limite inférieure unilatérale de 100(1 – α)% a la formule suivante :
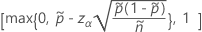
La limite supérieure unilatérale de 100(1 – α)% a la formule suivante :
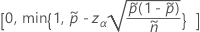
Pour les limites unilatérales, utilisez  dans la définition de
dans la définition de 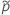 et
et 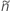 :
:
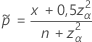
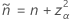
Test correspondant à l’intervalle d’Agresti-Coull
L’analyse calcule la valeur de p pour le test en inversant la procédure d’intervalle de confiance.
Notation
| Terme | Description |
|---|---|
| x | nombre d'événements |
| n | Nombre de répliques |
| zγ | le centile supérieur de la loi normale standard à γ |
| α | 1 – niveau de confiance / 100 |
Intervalle de confiance pour l’approximation de la normale de Wald (application Web)
Formule
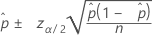
Notation
| Terme | Description |
|---|---|
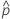 | probabilité observée, 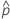 = x / n = x / n |
| x | nombre d'événements observé dans n essais |
| n | Nombre de répliques |
| zα/2 | probabilité cumulée inverse de la loi de distribution normale standard avec 1 – α/2 |
| α | 1 – niveau de confiance / 100 |