Équation de régression
Utilisez l’équation de régression pour décrire la relation entre la réponse et les termes du modèle. L’équation de régression est une représentation algébrique de la droite de régression. L’équation de régression du modèle linéaire se présente sous la forme suivante : Y= b0 + b1x1. Dans l’équation de régression, Y est la variable réponse, b0 est la constante ou l’ordonnée à l’origine, b1 est le coefficient estimé du terme linéaire (également appelé pente de la droite) et x1 est la valeur du terme.
L’équation de régression comportant plus d’un terme prend la forme suivante :
y = b0 + b1X1 + b2X2 + ... + bkXk
- y est la variable de réponse
- b0 est la constante
- b1, b2, ..., bk sont les coefficients
- X1, X2, ..., Xk sont les valeurs du terme. Chaque terme peut être un prédicteur unique, un terme polynomial ou un terme d’interaction.
Minitab utilise l’équation et les paramètres de la variable pour calculer l’ajustement.
Paramètres variables
Minitab utilise l’équation de régression et les paramètres de la variable pour calculer l’ajustement. Si les paramètres de la variable sont inhabituels par rapport aux données utilisées pour estimer le modèle, un avertissement s’affiche sous la prédiction.
Utilisez le tableau des paramètres de variable pour vérifier que vous avez effectué l’analyse comme prévu.
Valeur ajustée
Les valeurs ajustées sont également appelées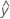 
. Les valeurs ajustées sont des estimations ponctuelles de la réponse moyenne des valeurs des prédicteurs. Les valeurs des prédicteurs sont également appelées valeurs de x. Minitab utilise l'équation de régression et les paramètres des variables pour calculer l'ajustement.
Le type de valeurs ajustées affichées par Minitab dépend du type de la variable de réponse de votre modèle. Par exemple, Minitab peut afficher des moyennes, des probabilités ou des écarts types selon le type de vos données : mesures continues ou de dénombrement, données binaires ou modèles utilisant la fonction Analyser la variabilité.
Interprétation
Les valeurs ajustées sont calculées en saisissant les valeurs X dans l'équation du modèle pour obtenir une variable de réponse.
Par exemple, si l'équation est y = 5 + 10x, la valeur ajustée pour la valeur X (2) est 25 (25 = 5 + 10(2)).
ErT ajust
L'erreur type de l'ajustement (ErT ajust) estime la variation de la réponse moyenne estimée pour les valeurs de variables spécifiées. Le calcul de l'intervalle de confiance de la réponse moyenne utilise l'erreur type de la valeur ajustée. Les erreurs types ne sont jamais négatives.
Interprétation
Utilisez l'erreur type de l'ajustement pour mesurer la précision de l'estimation de la réponse moyenne. Plus l'erreur type est faible, plus la prévision de la réponse moyenne est précise. Par exemple, un analyste développe un modèle pour prévoir des délais de livraison. Pour un ensemble de paramètres de variables, le modèle prévoit un délai de livraison moyen de 3,80 jours. L'erreur type de l'ajustement pour ces paramètres est de 0,08 jours. Pour un deuxième ensemble de paramètres de variables, le modèle produit le même délai de livraison moyen avec une erreur type de l'ajustement de 0,02 jours. Avec le second ensemble de paramètres de variables, l'analyste peut affirmer avec plus de certitude que le délai de livraison moyen est proche de 3,80 jours.
Avec la valeur ajustée, l'erreur type de l'ajustement permet de créer un intervalle de confiance pour la réponse moyenne. Par exemple, selon le nombre de degrés de liberté, un intervalle de confiance à 95 % s'étend approximativement sur deux erreurs types au-dessus ou en dessous de la moyenne prévue. Dans l'exemple des délais de livraison, pour la réponse moyenne prévue de 3,80 jours lorsque l'erreur type est de 0,08, l'intervalle de confiance à 95 % est (3,64 ; 3,96) jours. Vous pouvez être certain à 95 % que la moyenne de la population se situe à l'intérieur de cette étendue. Lorsque l'erreur type est de 0,02, l'intervalle de confiance à 95 % est (3,76 ; 3,84) jours. L'intervalle de confiance pour le second ensemble de paramètres de variables est plus étroit, car l'erreur type est plus faible.
IC à 95 %
L'intervalle de confiance pour la valeur ajustée fournit une étendue de valeurs possibles pour la réponse moyenne en fonction des paramètres spécifiés pour les prédicteurs.
Interprétation
Utilisez l'intervalle de confiance afin d'évaluer l'estimation de la valeur ajustée pour les valeurs observées des variables.
Par exemple, avec un niveau de confiance de 95 %, vous pouvez être sûr à 95 % que l'intervalle de confiance comprend la moyenne de la population pour les valeurs indiquées des variables du modèle. L'intervalle de confiance vous aide à évaluer la signification pratique de vos résultats. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation. Un grand intervalle de confiance traduit moins de certitude quant à la moyenne des futures valeurs. Si l'intervalle est trop grand pour être utile, vous devez sans doute augmenter votre effectif d'échantillon.
IP à 95 %
L'intervalle de prévision est une étendue ayant de fortes chances de contenir une réponse future pour une combinaison de paramètres de variables sélectionnée.
Interprétation
Utilisez les intervalles de prévision (IP) pour évaluer la précision des prévisions. Les intervalles de prévision vous aident à évaluer la signification pratique de vos résultats. Si un intervalle de prévision s'étend au-delà des limites acceptables, les prévisions peuvent ne pas être suffisamment précises pour vos exigences.
Avec un intervalle de prévision de 95 %, vous pouvez être certain à 95 % que la réponse unique figurera dans l'intervalle au vu des paramètres indiqués pour les prédicteurs. L'intervalle de prévision est toujours plus large que l'intervalle de confiance car la prévision d'une seule réponse comporte un plus grand degré d'incertitude que la prévision d'une réponse moyenne.
Par exemple, un ingénieur spécialisé dans les matériaux travaillant pour une entreprise de fabrication de meubles élabore un modèle de régression simple pour prévoir la rigidité d'un panneau de particules à partir de la densité du panneau. Il vérifie que le modèle satisfait aux hypothèses de l'analyse. L'analyste utilise ensuite le modèle pour prévoir la rigidité.
L'équation de régression prévoit que la rigidité pour une nouvelle observation avec une densité de 25 est égale à -21,53 + 3,541*25, soit 66,995. Bien qu'il soit peu probable qu'une telle observation ait une rigidité exacte de 66,995, l'intervalle de prévision indique que l'ingénieur peut être certain à 95 % que la valeur réelle sera comprise entre 48 et 86 environ.
