Un ingénieur en matériaux travaillant pour un fabricant de matériaux de construction développe un nouveau produit d'isolation. Il conçoit une expérience dans le cadre d'un plan factoriel complet à 2 niveaux, afin d'évaluer plusieurs facteurs pouvant influer sur la résistance, la densité et la qualité de l'isolation.
L'ingénieur ajuste le modèle de plan factoriel, puis il utilise la fonction Diagrammes factoriels pour mieux comprendre les effets.
- Ouvrez le fichier de données échantillons, PropriétésIsolation_modèle.MWX.
- Sélectionnez .
- Dans la fonction Réponse, sélectionnez Isolation.
- Sous Variables à inclure dans les diagrammes, déplacez Matériau, TempInj et TempRafr de la liste Disponibles vers la liste Sélectionnées.
- Cliquez sur OK.
Interprétation des résultats
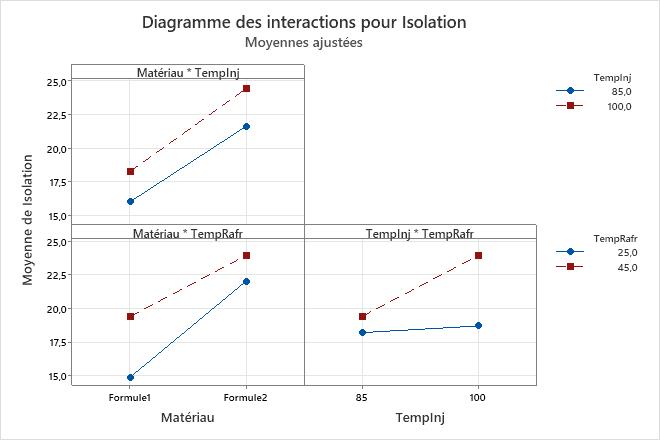
Le diagramme des interactions représente la moyenne ajustée de la valeur d'isolation par rapport aux combinaisons de matériau, de température d'injection et de température de rafraîchissement. Ce diagramme affiche des effets d'interaction apparents, car les lignes ne sont pas toutes parallèles, ce qui implique que la relation entre la valeur d'isolation et chaque facteur dépend du paramètre d'un autre facteur. Les résultats de la fonction Analyser un plan factoriel indiquent que les effets des interactions pour Matériau*TempRafr et TempInj*TempRafr sont statistiquement significatifs.
Le graphique des interactions de Matériau*TempRafr montre que l'effet de la température de refroidissement sur l'isolation est plus grand pour la Formule 1 que pour la Formule 2.
La relation entre la valeur d'isolation et la température d'injection dépend de la température de rafraîchissement. Lorsque le produit est fabriqué avec une température d'injection de 85°, la valeur d'isolation est presque identique pour les deux températures de rafraîchissement. Cependant, avec une température d'injection de 100°, la température de rafraîchissement est associée à des valeurs d'isolation très différentes. TempInj de 100° et TempRafr de 45° sont associées aux valeurs d'isolation les plus élevées.
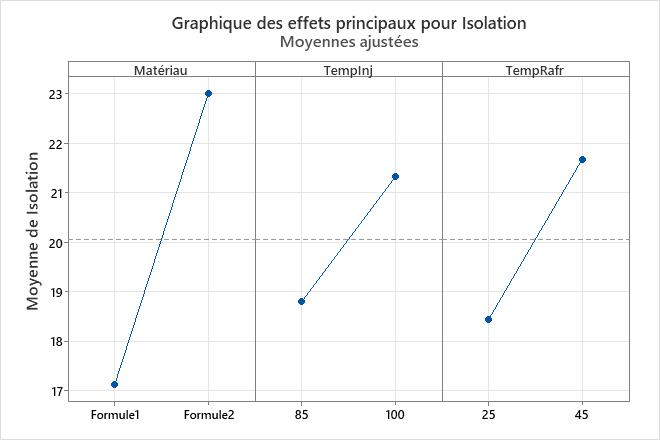
Les graphiques des effets principaux représentent les moyennes ajustées pour chaque niveau de chaque variable de catégorie. Les lignes n'étant pas horizontales, il existe des effets principaux pour toutes ces variables. Les résultats de la fonction Analyser un plan factoriel confirment que les effets principaux sont tous statistiquement significatifs. Toutefois, étant donné que les effets des interactions sont statistiquement significatifs, le graphique des effets principaux risque d'être trompeur. Aussi, vous ne pouvez pas interpréter les effets principaux sans tenir compte des effets des interactions.